算法原理
决策树（Decision Tree），可以认为是if-then规则的集合，其主要优点是模型具有可读性，分类速度快。决策树学习通常包括3个步骤：特征选择、决策树的生成、决策树的修剪。
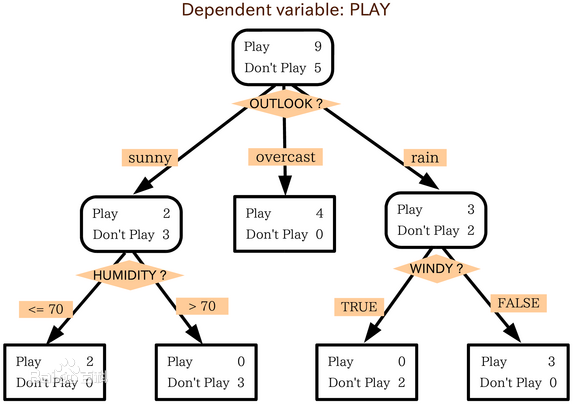
决策树的学习是一个递归的选择最优特征，然后根据该特征对训练数据进行分割的过程。为避免过拟合，还需要对生成的决策树进行剪枝。
信息增益大的特征具有更强的分类能力，信息增益的计算公式如下：g(D,A) = H(D) - H(D|A)。D表示训练数据集，A表示某一特征，H(D)表示D的熵，H(D|A)表示特征A给定的条件下D的熵。由于H(D)取决于训练样本，所以是个定值，要使g(D,A)大，那么H(D|A)必须小，也就是特征A给定的条件下D的信息量小，亦即特征A给定的条件下D发生的概率尽量大，考虑极端情况，特征A给定，D发生的概率为1，这时候仅仅用特征A即可拟合样本数据。
在介绍决策树算法之前我们先说一下熵的概念：熵表示某一事件是否发生这种不确定性的度量，假设某一事件E发生的概率为p，那么p越小获得的信息量越大，p趋于0时获得的信息量趋于无穷大，p等于1时信息量为0。熵的计算公式如下：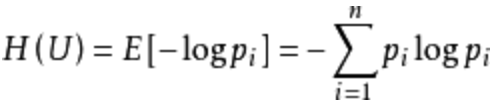
举个栗子，假如一个盒子里面有100个小球，99个白色的，1个黑色的，那么从中拿出黑色球的概率是1%，一旦从中拿出黑色球，就会给我们带来巨大的信息量（你会想，居然还有黑色球），黑色球带给我们的信息熵为-log(1/100)=4.605，而拿到白色小球的信息熵为-log(99/100)=0.01（因为每次都能大概率拿到白色球，再拿出白色球我都不会感到惊讶）。因为我们有1/100的概率拿到黑色球，99/100的概率拿到白色球，所以这盒小球带给我们的信息熵为：-(1/100)log(1/100)-(99/100)log(99/100) = 0.056。
下面我们看一下决策树的构建过程，考虑下面的数据表：
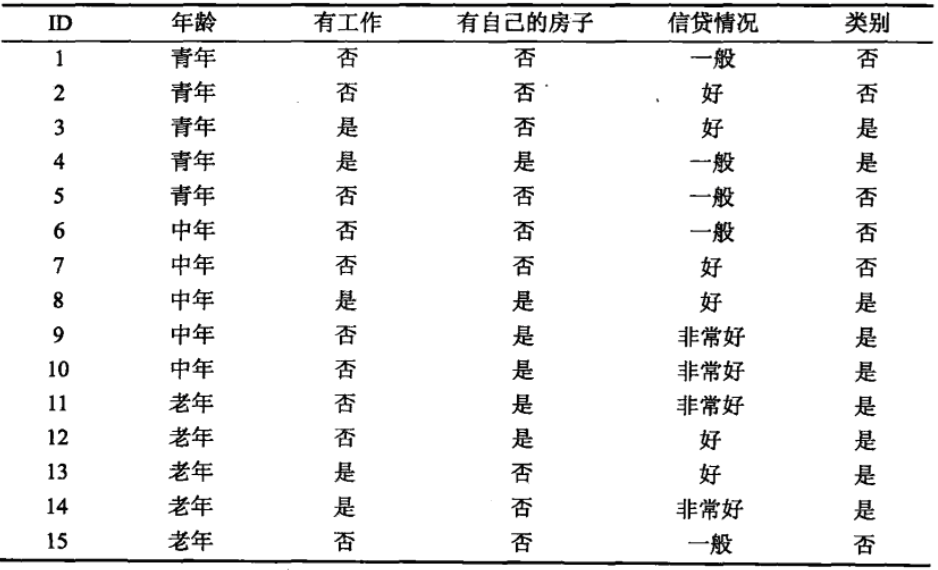我们选择信息增益最大的特征作为最优特征：
最后比较各特征的信息增益值，由于特征A3（有自己的房子）最大，所以选择A3作为最优特征，然后由该特征的不同取值作为分支子节点，再对子节点递归的调用以上方法，构建整颗决策树。
以上算法就是传说中的ID3算法，如果将上面过程中的信息增益量换成信息增益比，就是传说中的C4.5算法。
模型训练
代码地址 https://github.com/qianshuang/ml-exp
def train():
print("start training...")
# 处理训练数据
train_feature, train_target = process_file(train_dir, word_to_id, cat_to_id)
# 模型训练
model.fit(train_feature, train_target)
def test():
print("start testing...")
# 处理测试数据
test_feature, test_target = process_file(test_dir, word_to_id, cat_to_id)
# test_predict = model.predict(test_feature) # 返回预测类别
test_predict_proba = model.predict_proba(test_feature) # 返回属于各个类别的概率
test_predict = np.argmax(test_predict_proba, 1) # 返回概率最大的类别标签
# accuracy
true_false = (test_predict == test_target)
accuracy = np.count_nonzero(true_false) / float(len(test_target))
print()
print("accuracy is %f" % accuracy)
# precision recall f1-score
print()
print(metrics.classification_report(test_target, test_predict, target_names=categories))
# 混淆矩阵
print("Confusion Matrix...")
print(metrics.confusion_matrix(test_target, test_predict))
if not os.path.exists(vocab_dir):
# 构建词典表
build_vocab(train_dir, vocab_dir)
categories, cat_to_id = read_category()
words, word_to_id = read_vocab(vocab_dir)
# kNN
# model = neighbors.KNeighborsClassifier()
# decision tree
model = tree.DecisionTreeClassifier()
train()
test()
运行结果：
read_category...
read_vocab...
start training...
start testing...
accuracy is 0.822000
precision recall f1-score support
时政 0.69 0.67 0.68 94
房产 0.84 0.88 0.86 104
教育 0.72 0.72 0.72 104
娱乐 0.83 0.87 0.85 89
游戏 0.88 0.86 0.87 104
科技 0.88 0.89 0.88 94
家居 0.65 0.67 0.66 89
体育 0.98 0.92 0.95 116
财经 0.87 0.84 0.85 115
时尚 0.85 0.86 0.85 91
avg / total 0.82 0.82 0.82 1000
Confusion Matrix...
[[ 63 0 7 1 3 2 8 1 8 1]
[ 1 92 1 1 1 1 7 0 0 0]
[ 8 5 75 3 1 1 8 0 2 1]
[ 3 3 3 77 2 0 0 0 0 1]
[ 4 1 3 3 89 1 0 0 2 1]
[ 1 1 0 1 1 84 2 1 0 3]
[ 6 4 2 3 1 4 60 0 3 6]
[ 1 0 4 2 0 0 2 107 0 0]
[ 3 3 4 0 1 1 5 0 97 1]
[ 1 0 5 2 2 2 1 0 0 78]]
社群
- QQ交流群
- 微信交流群
- 微信公众号
