算法原理
AdaBoost（Adaptive Boosting）自适应Boosting算法，其核心思想是针对同一个训练集训练不同的分类器（弱分类器），然后把这些弱分类器集合起来，构成一个更强的最终分类器（强分类器）。AdaBoost算法本身是通过改变数据分布（样本权重和分类器权重）来实现的，它根据每次训练过程中，每个样本的分类结果是否正确来确定样本输入到下一分类器的权重，然后根据上一分类器的准确率，来确定分类器的权重。
使用加权后选取的训练数据代替随机选取的训练样本，这样将训练的焦点集中在比较难分的训练数据样本上；将弱分类器联合起来，使用加权的投票机制代替平均投票机制，让分类效果好的弱分类器具有较大的权重，而分类效果差的分类器具有较小的权重。
下面我们通过一个实例来详细讨论一下AdaBoost的算法原理。考虑下面的数据分布，图中“+”和“-”表示两种类别，我们用水平或者垂直的直线作为基分类器（sk-learn库中，基分类器默认是决策树）。
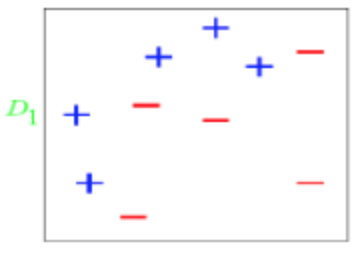
- 算法开始前默认均匀分布D，且正负样本数量相等，共10个样本，故每个样本权值为0.1。
- 先进行第一次分类，这第一个分类器有3个点划分错误，根据误差表达式计算可得e1=(0.1+0.1+0.1)/1.0=0.3。
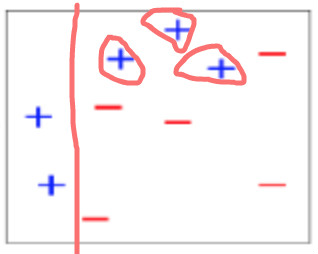
- 根据e1计算分类器权重（通过最小化损失函数推导而来）：
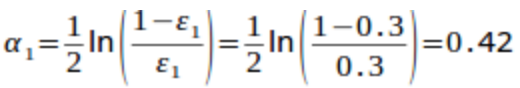。然后计算样本点权重：对于正确分类的7个点，权值不变，仍为0.1；对于错分的3个点，权值为：W0(1-e1)/e1=0.1(1-0.3)/0.3=0.2333。 - 再进行第二次分类，如图所示，有3个”-“分类错误，上轮分类过后权值之和为：0.17+0.23333=1.3990，所以分类误差e2=0.13/1.3990=0.2144，同样根据公式计算这第二个基分类器权重a2=0.6493，错分的3个点权值为0.1（1-0.2144）/0.2144=0.3664。
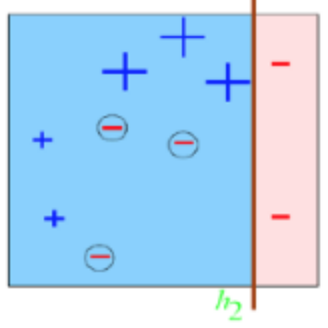
- 最后进行第三次分类，同上步骤可求得：e3=0.1365；a3=0.9223；D3=0.6326。
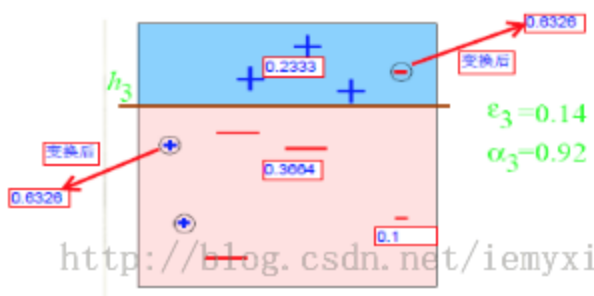
- 最终的强分类器即为三个弱分类器的叠加：
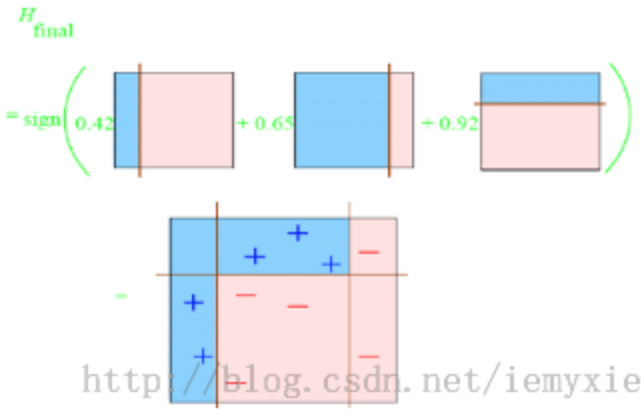
以上就是AdaBoost的算法原理，Adaboost实际上提供的是框架，我们可以使用各种方法构建基分类器，但是该算法对噪声点异常敏感，噪声点在迭代中可能会获得较高的权重，从而影响最终的强学习器的预测准确性。
从损失函数的角度看，AdaBoost的损失函数L(y,f(x)) = exp[-y*f(x)]，其中y取值1或-1（代表二分类的类别标签），f(x) = a1 * G1(x) + a2 * G2(x) + …，是AdaBoost的最终分类器表达式。
模型训练
代码地址 https://github.com/qianshuang/ml-exp
def train():
print("start training...")
# 处理训练数据
train_feature, train_target = process_file(train_dir, word_to_id, cat_to_id)
# 模型训练
model.fit(train_feature, train_target)
def test():
print("start testing...")
# 处理测试数据
test_feature, test_target = process_file(test_dir, word_to_id, cat_to_id)
# test_predict = model.predict(test_feature) # 返回预测类别
test_predict_proba = model.predict_proba(test_feature) # 返回属于各个类别的概率
test_predict = np.argmax(test_predict_proba, 1) # 返回概率最大的类别标签
# accuracy
true_false = (test_predict == test_target)
accuracy = np.count_nonzero(true_false) / float(len(test_target))
print()
print("accuracy is %f" % accuracy)
# precision recall f1-score
print()
print(metrics.classification_report(test_target, test_predict, target_names=categories))
# 混淆矩阵
print("Confusion Matrix...")
print(metrics.confusion_matrix(test_target, test_predict))
if not os.path.exists(vocab_dir):
# 构建词典表
build_vocab(train_dir, vocab_dir)
categories, cat_to_id = read_category()
words, word_to_id = read_vocab(vocab_dir)
# kNN
# model = neighbors.KNeighborsClassifier()
# decision tree
# model = tree.DecisionTreeClassifier()
# random forest
# model = ensemble.RandomForestClassifier(n_estimators=10) # n_estimators为基决策树的数量，一般越大效果越好直至趋于收敛
# AdaBoost
model = ensemble.AdaBoostClassifier(learning_rate=1.0) # learning_rate的作用是收缩基学习器的权重贡献值
train()
test()
运行结果：
read_category...
read_vocab...
start training...
start testing...
accuracy is 0.801000
precision recall f1-score support
财经 0.93 0.80 0.86 115
体育 0.99 0.97 0.98 116
娱乐 0.95 0.78 0.85 89
科技 0.94 0.89 0.92 94
时尚 0.89 0.92 0.91 91
房产 0.85 0.82 0.83 104
教育 0.75 0.68 0.71 104
游戏 0.86 0.85 0.85 104
家居 0.57 0.55 0.56 89
时政 0.45 0.71 0.55 94
avg / total 0.82 0.80 0.81 1000
Confusion Matrix...
[[ 92 0 0 0 0 1 4 0 2 16]
[ 0 112 0 0 0 0 2 0 2 0]
[ 0 0 69 0 1 2 3 12 0 2]
[ 0 0 0 84 1 0 0 0 5 4]
[ 0 0 1 1 84 0 1 1 2 1]
[ 0 0 0 0 1 85 2 0 2 14]
[ 1 1 1 1 2 3 71 0 6 18]
[ 0 0 1 0 1 2 1 88 6 5]
[ 2 0 1 2 2 7 3 1 49 22]
[ 4 0 0 1 2 0 8 0 12 67]]
社群
- QQ交流群
- 微信交流群
- 微信公众号
