算法原理
朴素贝叶斯（Naive Bayes）是基于贝叶斯定理与特征条件独立假设的分类算法。首先假设特征与特征之间互相独立，然后利用贝叶斯定理求出后验概率最大的输出y。
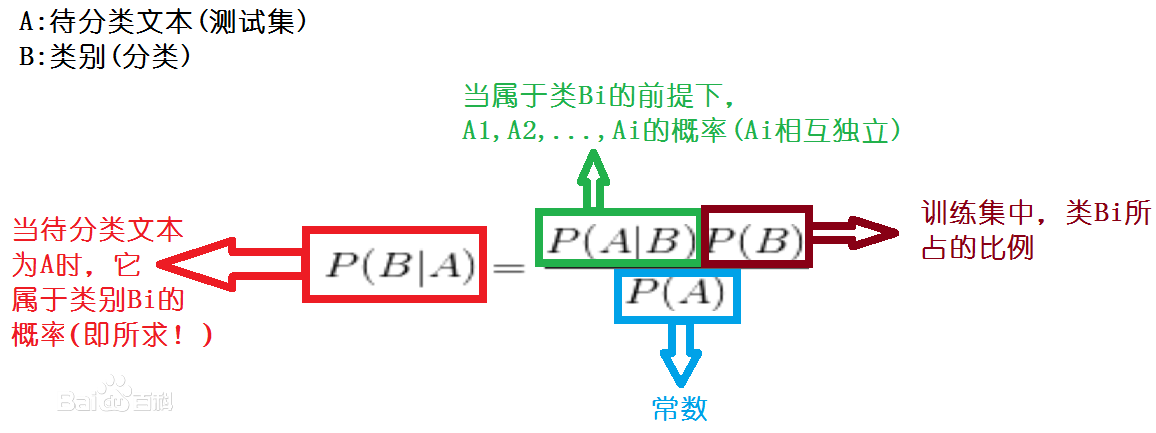其中，P(B)是类先验概率，P(A|B)是样本A相对于类标记B的类条件概率，P(A)是用于归一化的证据因子，表示我从无数样本中得到这个训练样本的概率，是一个定值，所以我们只需要求出P(A|B)即可。
由于P(A|B) = P(A1,A2,A3,,,,,,An|B)，A1,An表示特征（也就是我们的词频），由于朴素贝叶斯假定特征之间相互独立，所以P(A1,A2,A3,,,,,,An|B) = P(A1|B)*P(A2|B)*......*P(An|B)。P(An|B)表示的意思是在类别B中，特征An出现的概率，也就是An出现的次数除以总字数。
下面我们通过一个实际的例子，看一下朴素贝叶斯的具体算法原理：
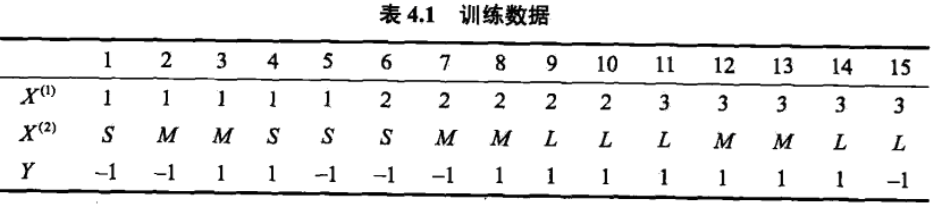
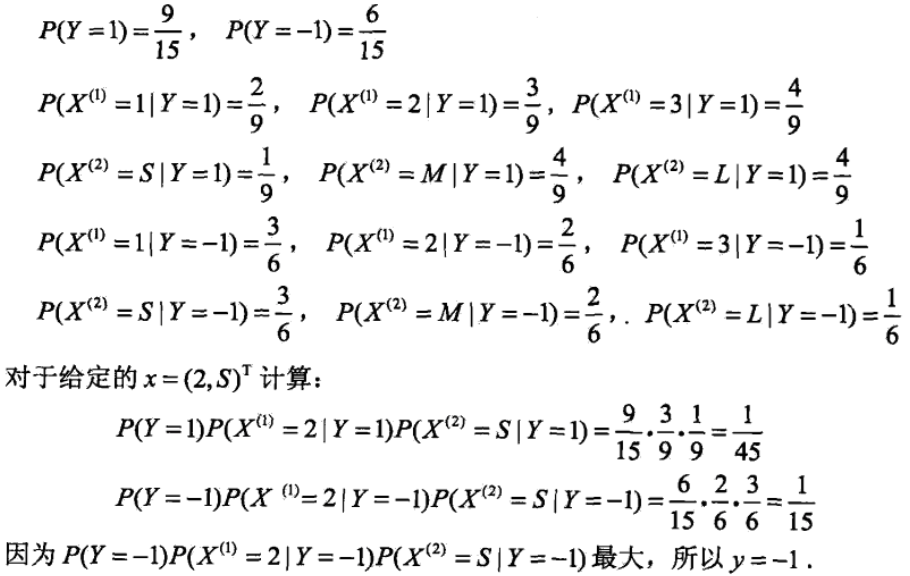注意，如果某个属性值在训练集中没有与某个类同时出现过，则直接基于上面的公式会出现很多概率为0的情况，为了避免其他属性携带的信息被训练集中未出现的属性值抹去（概率很小不等于说没有概率），在估计概率时通常要进行平滑，常用的是拉普拉斯平滑，这时候P(B) = (Db+1)/(D+N);P(An|B) = (Dbn+1)/(Db+Nn)，N表示训练集D中所有的类别数量，Nn表示第n个属性可能的取值数。
下面我们重新使用拉普拉斯平滑估计概率：
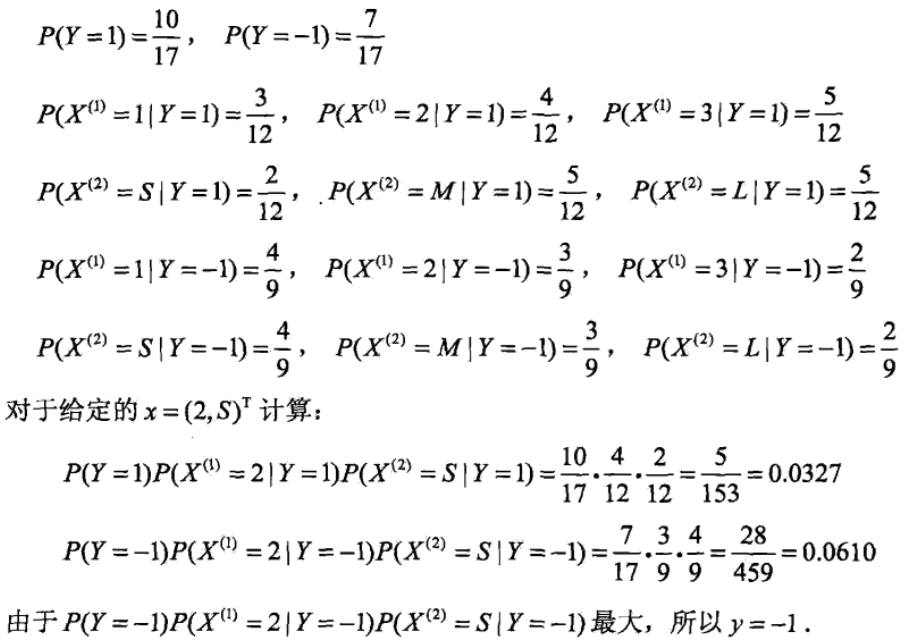拉普拉斯平滑避免了因训练集样本不充分而导致概率估值为0的问题，并且在训练集变大时，平滑过程所引入的先验的影响也会逐渐变得可忽略，使得估值渐趋向于实际概率值。
贝叶斯网络学习的首要任务是根据训练数据集，找出结构最恰当的贝叶斯网。如下图，c：抽烟；a：肺癌；b：支气管炎。
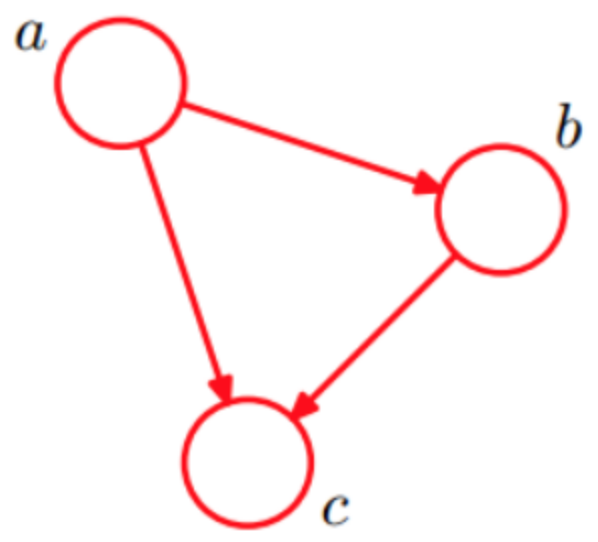p(a,b,c) = p(c|a,b) * p(b|a) * p(a)
如果把上面图的边去掉，那么p(a,b,c) = p(a) * p(b) * p(c)，这就变成朴素贝叶斯的特征独立假定了，所以朴素贝叶斯是贝叶斯网络的特例。
特殊的贝叶斯网络：隐马尔科夫模型
TF-IDF，TF(Term Frequency)表示词频，一篇文档中每个词语出现的次数，通常还需要除以文章总词数做归一化，以防止它偏向长的文件；IDF（inverse document frequency）逆文档频率，用来描述一个词的重要程度，也就是词权重。TF-IDF = TF * IDF，相当于给词本身带上了权重值。idf计算公式：
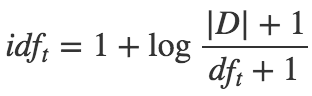D表示文档总数，是一个常数，df表示该词一共在多少篇文档中出现过，三处加1是平滑处理。
模型训练
代码地址 https://github.com/qianshuang/ml-exp
def train():
print("start training...")
# 处理训练数据
# train_feature, train_target = process_file(train_dir, word_to_id, cat_to_id) # 词频特征
train_feature, train_target = process_tfidf_file(train_dir, word_to_id, cat_to_id) # TF-IDF特征
# 模型训练
model.fit(train_feature, train_target)
def test():
print("start testing...")
# 处理测试数据
test_feature, test_target = process_file(test_dir, word_to_id, cat_to_id)
# test_predict = model.predict(test_feature) # 返回预测类别
test_predict_proba = model.predict_proba(test_feature) # 返回属于各个类别的概率
test_predict = np.argmax(test_predict_proba, 1) # 返回概率最大的类别标签
# accuracy
true_false = (test_predict == test_target)
accuracy = np.count_nonzero(true_false) / float(len(test_target))
print()
print("accuracy is %f" % accuracy)
# precision recall f1-score
print()
print(metrics.classification_report(test_target, test_predict, target_names=categories))
# 混淆矩阵
print("Confusion Matrix...")
print(metrics.confusion_matrix(test_target, test_predict))
if not os.path.exists(vocab_dir):
# 构建词典表
build_vocab(train_dir, vocab_dir)
categories, cat_to_id = read_category()
words, word_to_id = read_vocab(vocab_dir)
# kNN
# model = neighbors.KNeighborsClassifier()
# decision tree
# model = tree.DecisionTreeClassifier()
# random forest
# model = ensemble.RandomForestClassifier(n_estimators=10) # n_estimators为基决策树的数量，一般越大效果越好直至趋于收敛
# AdaBoost
# model = ensemble.AdaBoostClassifier(learning_rate=1.0) # learning_rate的作用是收缩基学习器的权重贡献值
# GBDT
# model = ensemble.GradientBoostingClassifier(n_estimators=10)
# xgboost
# model = xgboost.XGBClassifier(n_estimators=10)
# Naive Bayes
model = naive_bayes.MultinomialNB()
train()
test()
运行结果：
read_category...
read_vocab...
start training...
start testing...
accuracy is 0.915000
precision recall f1-score support
体育 0.98 0.94 0.96 116
科技 0.99 0.99 0.99 94
财经 0.97 0.96 0.96 115
家居 0.87 0.80 0.83 89
时尚 0.98 0.89 0.93 91
游戏 1.00 0.92 0.96 104
时政 0.88 0.87 0.88 94
娱乐 0.89 0.96 0.92 89
教育 0.82 0.90 0.86 104
房产 0.80 0.90 0.85 104
avg / total 0.92 0.92 0.92 1000
Confusion Matrix...
[[109 0 0 0 0 0 1 0 5 1]
[ 0 93 0 1 0 0 0 0 0 0]
[ 0 0 110 1 0 0 2 0 0 2]
[ 1 0 1 71 1 0 1 1 2 11]
[ 0 0 0 3 81 0 0 4 3 0]
[ 0 1 0 1 0 96 0 1 5 0]
[ 0 0 1 0 0 0 82 0 1 10]
[ 0 0 0 0 0 0 1 85 3 0]
[ 1 0 0 2 1 0 2 4 94 0]
[ 0 0 1 3 0 0 4 1 1 94]]
社群
- QQ交流群
- 微信交流群
- 微信公众号
