损失函数



 所以,线性回归先假定特证满足线性关系,然后根据给定的训练数据,求出使损失函数(均方误差)最小时的参数k和b的解析解,这就是线性回归的训练过程。下面我们举个实际的例子,看看线性回归模型到底是怎样进行训练求出参数k和b的。我们假设商品的销售量和商品单价满足线性关系:y=kx+b,x为商品的单价,y代表商品的销售量。现在我们收集到的线上样本如下:
所以,线性回归先假定特证满足线性关系,然后根据给定的训练数据,求出使损失函数(均方误差)最小时的参数k和b的解析解,这就是线性回归的训练过程。下面我们举个实际的例子,看看线性回归模型到底是怎样进行训练求出参数k和b的。我们假设商品的销售量和商品单价满足线性关系:y=kx+b,x为商品的单价,y代表商品的销售量。现在我们收集到的线上样本如下:
| 单价x | 销量y |
|---|---|
| 1 | 2.5 |
| 2 | 5.5 |
| 3 | 6.5 |
根据训练样本训练一个线性回归模型?
大家回忆一下AdaBoost和GDBT的损失函数:AdaBoost为指数损失,GDBT为平方损失,逻辑回归是对数损失。
梯度下降
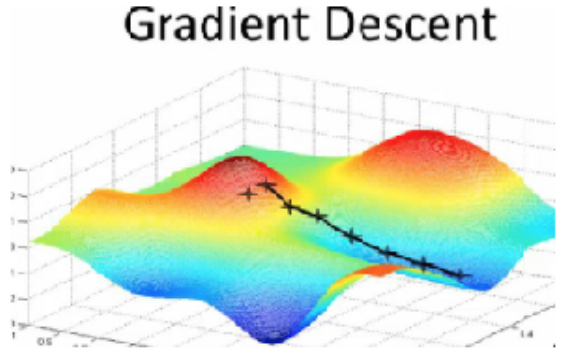 假设你深处一座大山高处,迷雾蒙蒙,完全看不清前路,你唯一能看到的就是你脚下的坡度,这时候怎样能够尽快逃出迷雾呢?最好的方式就是每次沿着当前最陡的坡度迈步,一旦坡度为0,也就到达了山底,这就是梯度下降。
还有一个很重要的参数就是步长(learning rate),如果步长太小,就需要很长时间(很多次迭代)才能到达山底;如果步长太大,很可能越过了当前的最低点,导致在最低点两侧摆动,但是这也有可能导致探索出新的最低点。
梯度下降是万能药水,我们在做损失函数最小化求模型参数时,并不是所有的函数都像线性回归一样能顺利求出解析解的(比如我们下节课要讲的逻辑回归和softmax回归),这时一般就可以用梯度下降法求解:
假设你深处一座大山高处,迷雾蒙蒙,完全看不清前路,你唯一能看到的就是你脚下的坡度,这时候怎样能够尽快逃出迷雾呢?最好的方式就是每次沿着当前最陡的坡度迈步,一旦坡度为0,也就到达了山底,这就是梯度下降。
还有一个很重要的参数就是步长(learning rate),如果步长太小,就需要很长时间(很多次迭代)才能到达山底;如果步长太大,很可能越过了当前的最低点,导致在最低点两侧摆动,但是这也有可能导致探索出新的最低点。
梯度下降是万能药水,我们在做损失函数最小化求模型参数时,并不是所有的函数都像线性回归一样能顺利求出解析解的(比如我们下节课要讲的逻辑回归和softmax回归),这时一般就可以用梯度下降法求解:
 参数theta的梯度推导公式如下(注意负梯度):
参数theta的梯度推导公式如下(注意负梯度):
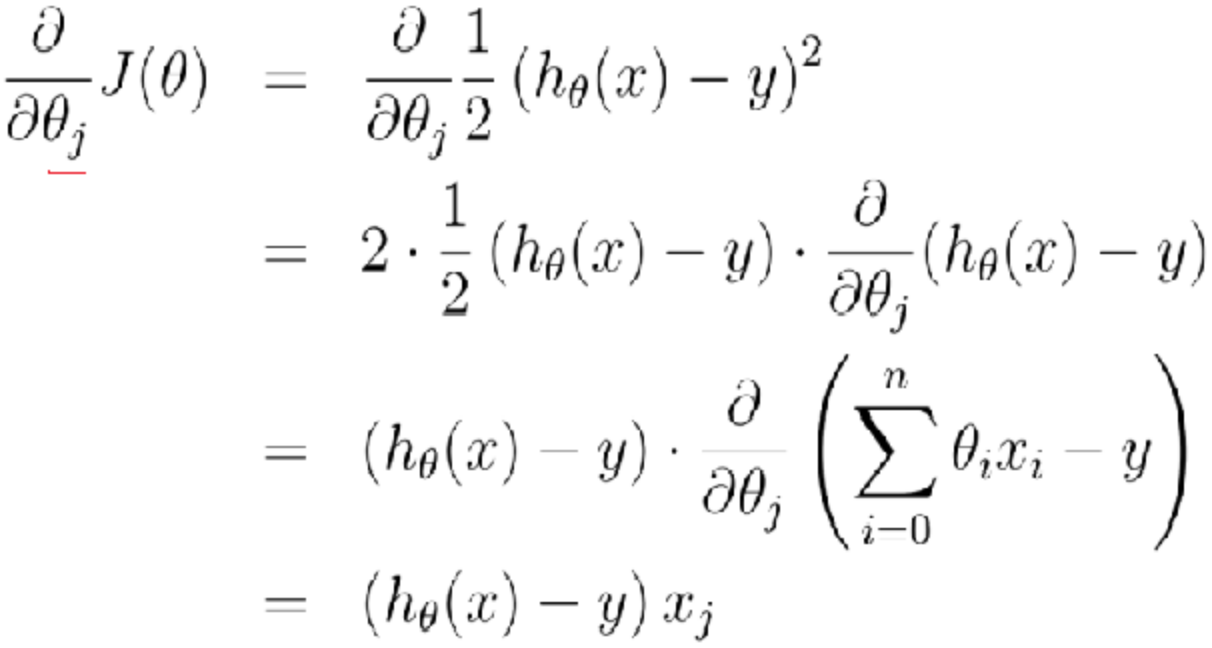
梯度下降一般有三种方式:批量梯度下降(Batch Gradient Descent)、随机梯度下降(Stochastic Gradient Descent)、Mini-batch Gradient Descent。
批量梯度下降要求每次计算使用所有的训练数据来更新模型参数。所以当训练数据量很大时迭代速度会非常慢,甚至内存溢出,优点是每次找的都是全局最优点。
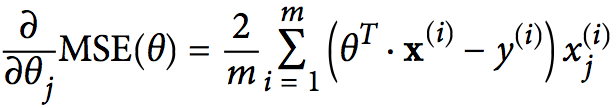 随机梯度下降每次从训练样本中随机采样一部分用来更新模型参数,并且每次更新时,只使用一个样本。所以模型的迭代速度很快,即使当训练数据量很庞大时,也能完成训练,并且随机采样有助于越过局部最优从而最终找到全局最优点,但是同样因为是随机,可能导致不能很平滑的到达局部最优,而是摇摇晃晃额到达。通常的解决方式是通过learning rate decay,即周期性的缩小learning rate。
随机梯度下降每次从训练样本中随机采样一部分用来更新模型参数,并且每次更新时,只使用一个样本。所以模型的迭代速度很快,即使当训练数据量很庞大时,也能完成训练,并且随机采样有助于越过局部最优从而最终找到全局最优点,但是同样因为是随机,可能导致不能很平滑的到达局部最优,而是摇摇晃晃额到达。通常的解决方式是通过learning rate decay,即周期性的缩小learning rate。
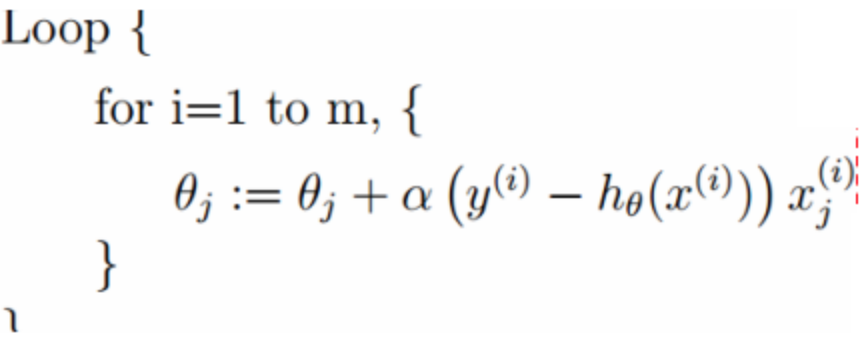 Mini-batch Gradient Descent综合了批量和随机梯度下降的有点,即每个epoch先对训练数据集做shuffle(相当于随机操作),然后分成n份,每次迭代使用一份训练子集。
Mini-batch Gradient Descent综合了批量和随机梯度下降的有点,即每个epoch先对训练数据集做shuffle(相当于随机操作),然后分成n份,每次迭代使用一份训练子集。
下面我们还是通过上面商品销量的例子,使用批量梯度下降法训练模型参数?(b –> b + a(t-y))
最大似然估计
想象我们站在阿里巴巴公司大楼观察大门口的来往人群,现在我们想训练这个来往人群模型,在我们观察的样本中,有六个男的,四个女的,所以模型需要最大化的拟合观测情况,如果模型的预测值是8个男的,2个女的,那就与我们的观测情况严重不符,这就是极大似估计。通过最大化似然求解模型参数的过程就是最大似然估计算法。

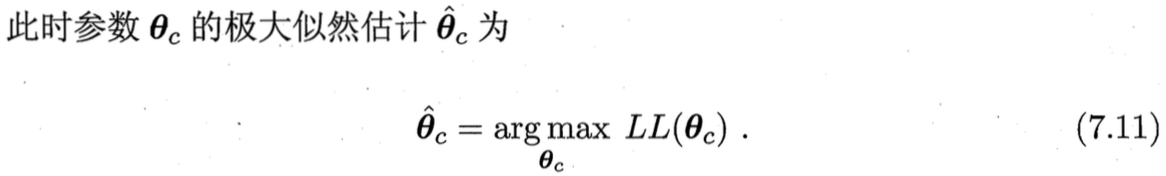 下面通过一个实际例子感受一下最大似然估计算法的魅力。
在抛硬币实验中,假设连续抛掷了10次硬币,结果为:+ - + - + + - + + -,求这枚硬币出现正面的概率?
下面通过一个实际例子感受一下最大似然估计算法的魅力。
在抛硬币实验中,假设连续抛掷了10次硬币,结果为:+ - + - + + - + + -,求这枚硬币出现正面的概率?
正则化
有一种特殊的线性回归叫polynomial regression,多项式回归,它将输入特征乘n次方作为新的特征训练线性回归模型,即将y = kx + b变换为y = k2x^2 + k1x + b,所以这种方式既可以拟合线性模型也可以拟合非线性模型。那么这个n到底取多少合适呢?一旦过大就会出现过拟合现象:
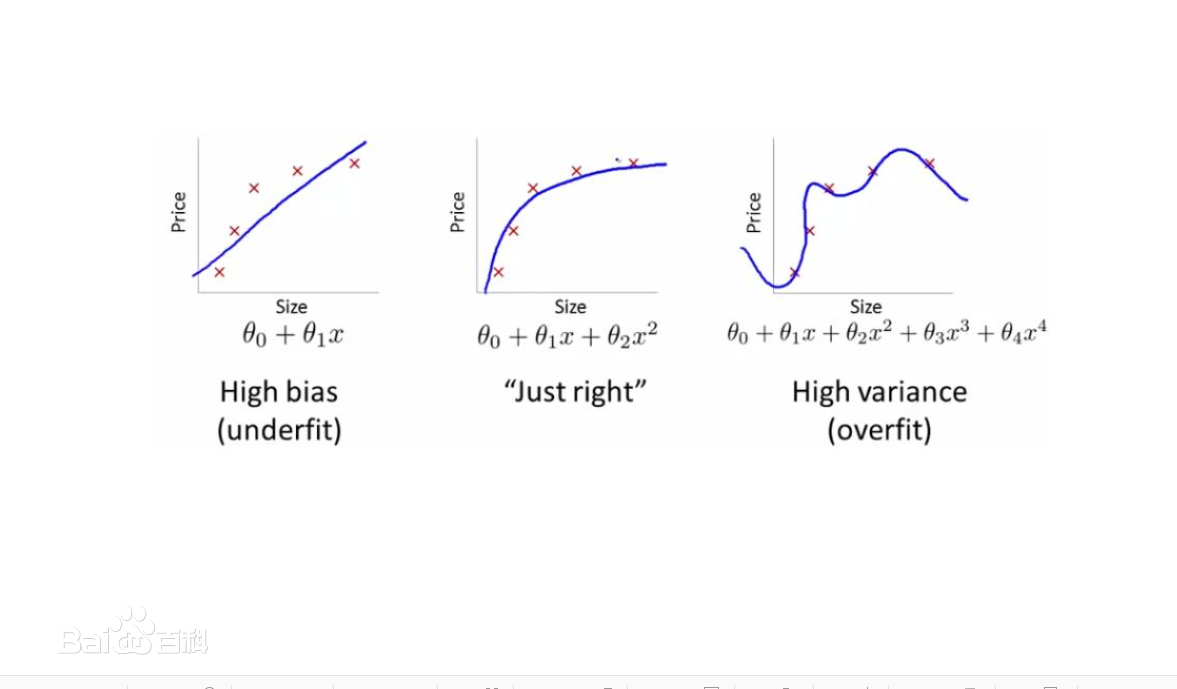 正则化是用来解决过拟合的重要手段之一,可以用来约束模型的参数值不至于过大,主要有三种方式:Ridge Regression,即通常所说的L2正则;Lasso Regression,即L1正则;Elastic Net,是Ridge和Lasso的综合。
正则化是用来解决过拟合的重要手段之一,可以用来约束模型的参数值不至于过大,主要有三种方式:Ridge Regression,即通常所说的L2正则;Lasso Regression,即L1正则;Elastic Net,是Ridge和Lasso的综合。
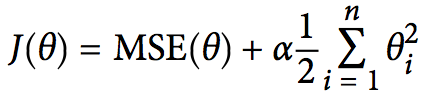
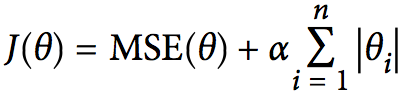
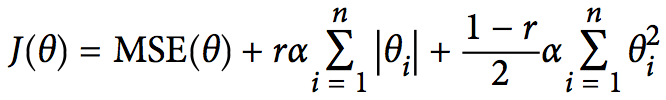 一般来说,L1正则化使参数(特征)更加稀疏,导致优化后的参数一部分为0,而另一部分非零实值即是选择后的重要参数(重要特征维度),所以也起到了去除噪声的效果;L2正则化使权重平滑,且这些特征都会接近于较小的0值。这背后的根本原因在于,一般权重值都在(-1,1)之间,w^2远小于w,所以L2正则允许保留较多的权重值。
一般来说,L1正则化使参数(特征)更加稀疏,导致优化后的参数一部分为0,而另一部分非零实值即是选择后的重要参数(重要特征维度),所以也起到了去除噪声的效果;L2正则化使权重平滑,且这些特征都会接近于较小的0值。这背后的根本原因在于,一般权重值都在(-1,1)之间,w^2远小于w,所以L2正则允许保留较多的权重值。
还有一种用来防止模型过拟合的重要正则化手段是Early Stopping,即一旦模型在验证集上的效果达到最佳(比如1000轮没有效果提升),立即停止训练,否则很可能出现过拟合。
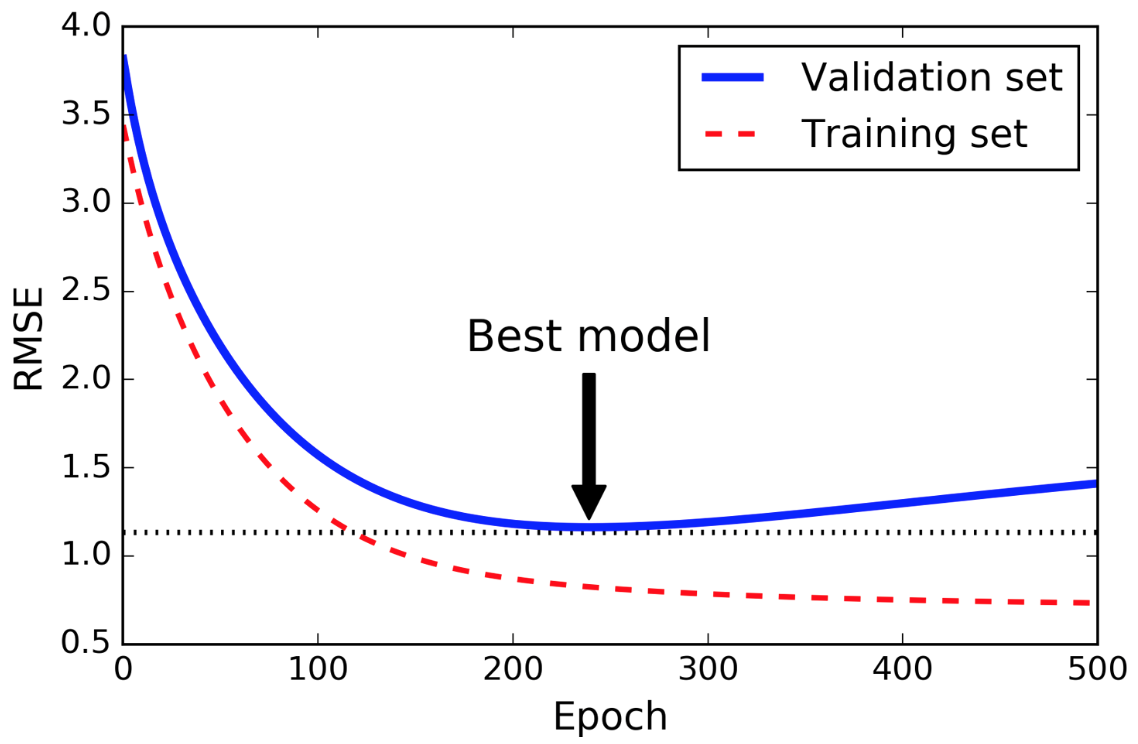
另外,随机和dropout也是防止模型过拟合的重要正则化手段。
社群
- QQ交流群

- 微信交流群

- 微信公众号
