算法原理
概率图模型是一类用图来表达变量之间相关关系的概率模型。马尔科夫网络假设随机过程中各个状态St的概率分布，只与他的前一个状态有关，即P(St|S1,S2,…,St-1) = P(St|St-1)，所以可以认为马尔科夫网络是一种特殊的贝叶斯网络。
隐马尔科夫模型是含有隐变量的马尔科夫网络，该模型包含两种类型的变量：一种是观测变量{x1,x2,…,xn}，表示第i时刻的观测值；一种是状态变量{y1,y2,…,yn}，即隐变量，表示第i时刻的状态。
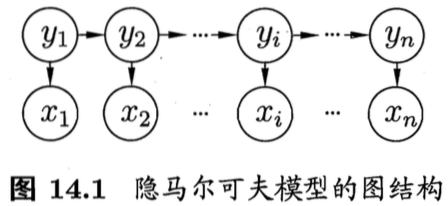所以所有变量的联合概率分布为：
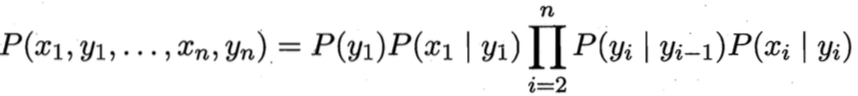
要确定一个隐马尔科夫模型，需要三组参数：λ = [A, B, π]。
A是状态转移概率矩阵，矩阵的每个元素表示由状态St转移到St+1的概率：
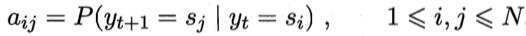B是输出观测概率矩阵，矩阵的每个元素表示根据当前状态St，获得各个观测值Oj的概率：
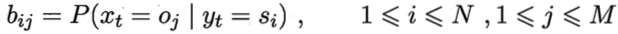π是初始状态概率矩阵，表示模型在初始时刻各状态出现的概率：
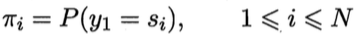下面举个例子方便大家理解整个过程：
在实际应用中，人们常常关注的是隐马尔科夫模型的三个基本问题：
- 给定模型计算观测序列发生的概率即为第一个问题。
- 在语音识别任务中，观测值是语音信号，隐藏状态为文字，我们目标就是根据语音信号来推测最有可能的文字序列，这即是第二个问题。
- 大多数现实任务中，模型的参数是要根据训练样本学习得到，这恰好是第三个问题。
这三个问题都有特别高效的解法。 对于第一个概率计算问题，可以通过前向后向算法直接计算得到，比较简单，这里不再赘述。
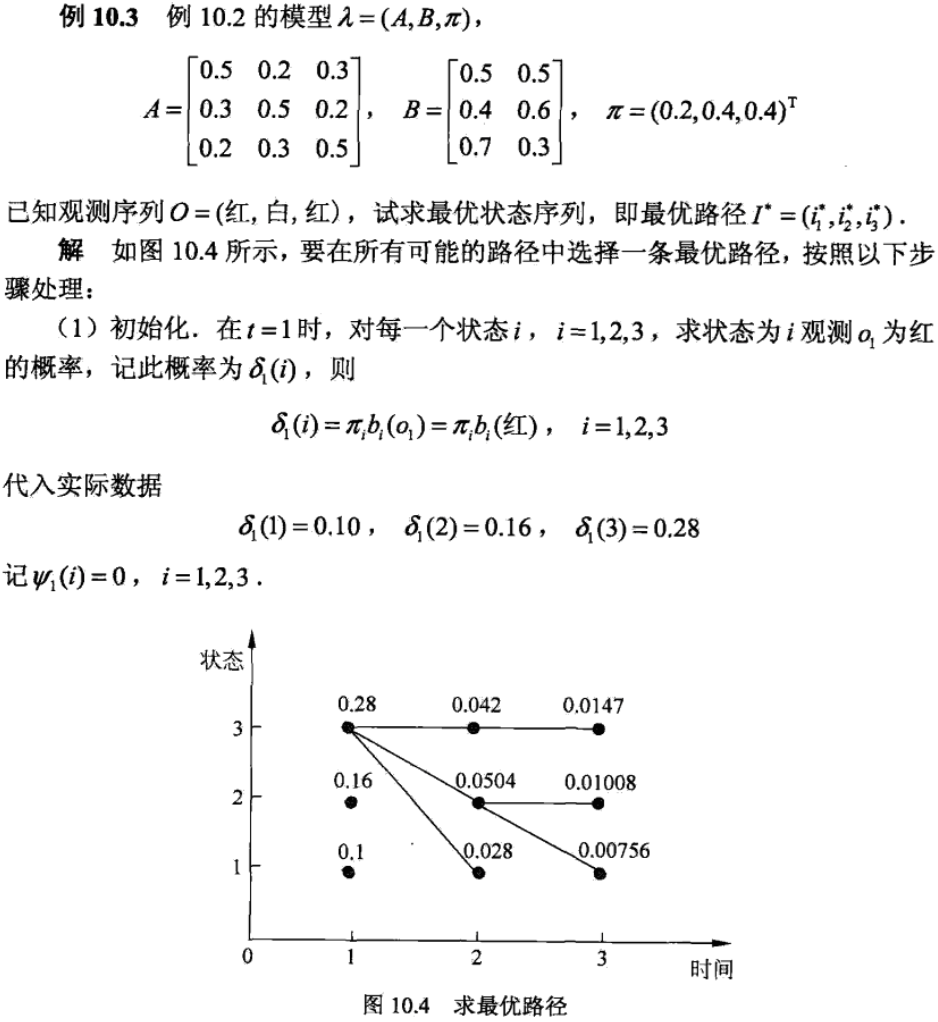
对于第二个根据观测序列推测最优的状态序列，可以通过维特比算法求解。维特比算法实际上是利用动态规划求概率最大路径（最短路径）问题。下面还是通过一个例子介绍著名的维特比算法。
对于第三个HMM模型训练问题，根据训练数据是包括观测序列和对应的状态序列还是只有观测序列，可以分别用有监督学习和无监督学习实现。 因为有监督学习的训练数据已做好了标注，所以直接统计就可以求出λ = [A, B, π]各参数值，实际应用中我们一般使用效果更好的CRF算法。关于CRF算法的具体原理请看下一节内容：条件随机场 而对于无监督的情况，也就是在只有观测序列的情况下（状态序列为隐变量），我们可以用EM算法求解模型参数。关于EM算法的具体原理请看第15节内容：期望最大化
社群
- QQ交流群
- 微信交流群
- 微信公众号
