算法原理
EM
期望最大化（Expectation Maximizition，EM），在前面的讨论中，我们一直假设训练样本所有属性变量的值都已被观测到，即训练样本是完整的，但是在现实应用中，往往会遇到不完整的训练样本，即我们知道有一个属性变量对模型至关重要，但是无法获得这个属性变量的值。在这种存在未观测变量（隐变量）的情形下，是否仍能对模型参数进行估计呢？
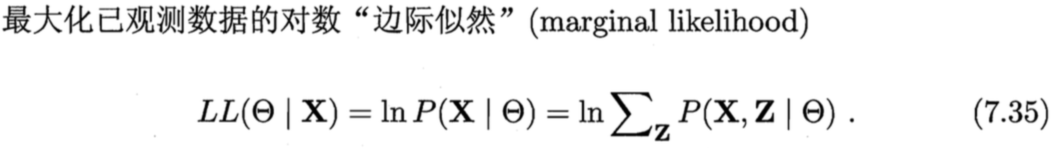EM算法是常用的在含有隐变量的情况下，估计模型参数的利器（训练完成后最终还可以求得隐变量的参数值）。其基本思想是：
- 首先初始化模型参数θ；
- 然后根据训练数据和当前的模型参数θ推断出最优隐变量Z的值（即求Z的期望，E步）；
- 基于训练数据和Z的最优期望值对参数θ做极大似然估计（M步）；
- 迭代的将2、3交替进行，直到收敛到局部最优解。
由于会收敛到局部最优解，EM算法对初值敏感，对于不同的初始值，可能会导致不同的结果，并且它对于“躁声”和孤立点数据也是敏感的，少量的该类数据能够对模型产生极大的影响。
实际上若隐变量的情况已知，那么我们可以直接根据最大似然估计和随机梯度下降，解出在每一种隐变量情况下的参数和最大似然估计值，然后选择似然估计最大情况下的模型和隐变量。
举例：考虑数据集D是一个实例集合，它由k个不同的正态分布的混合分布所生成（如下图k等于2），现在通过EM算法训练求解此混合高斯模型？
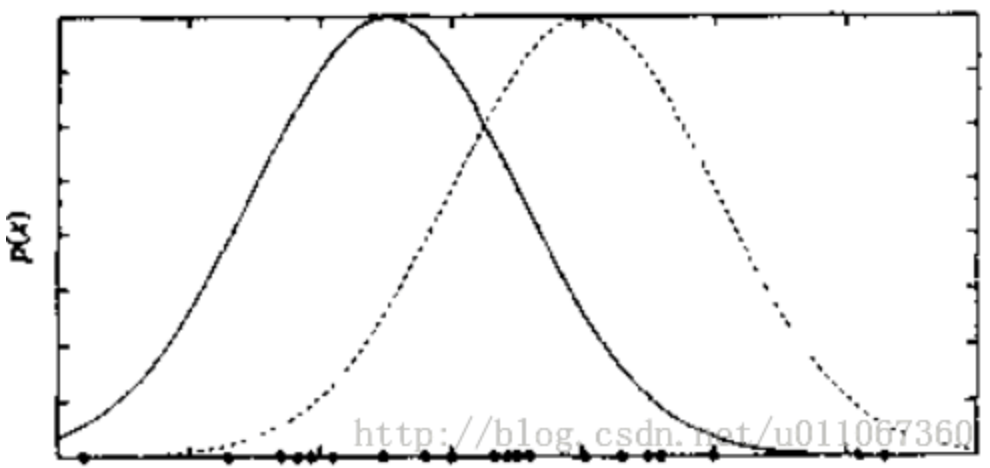这里可把每个实例的完整描述看作是一个三元组<xi,zi1, zi2>，其中xi是第i个实例的观测值，zi1和zi2表示两个正态分布中哪个被用于产生值xi，确切地讲，zij在xi由第j个正态分布产生时值为1，否则为0，可见zi1和zi2是隐藏变量。算法步骤如下：
- 首先初始化模型参数h=<μ1,μ2>（两个高斯模型的均值）；
- 根据当前的模型，计算每个隐藏变量zij的期望值E[zij]（最优值，可由将当前值<μ1,μ2>和所有样本点代入到下式中计算得到）；
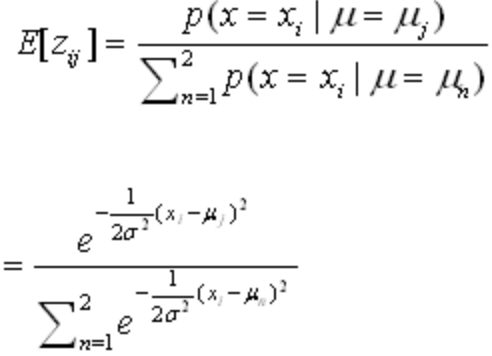
- 使用上步中得到的E[zij]来计算新的极大似然参数h´=<μ1´,μ2´>（其实是对μj的加权样本均值）；
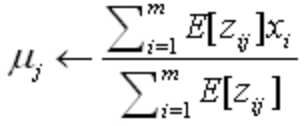
- 迭代的将2、3交替进行，直到收敛到局部最优解。
k-means
聚类是一种最典型的无监督学习任务，而k-means聚类是所有聚类算法的典型。
直接最小化式(9.24)并不容易，找到它的最优解需要考察样本集D所有可能的簇划分，这是一个NP难问题，因此k-means算法采用了贪心策略，通过迭代优化来近似求解式(9.24)，算法流程如下：
- 从D中随机选择k个样本作为初始质心；（k为超参数）
- 将所有样本点归类到距离质心最近的簇中；
- 重新计算簇的质心作为新的质心；
- 迭代的将2、3交替进行，直到收敛到局部最优解。
可以发现，k-means算法和EM算法原型惊人的相似，其实k-means就是EM算法的一种特殊实现。我们的模型参数是簇的质心，根据簇的质心将所有样本点归类到距离质心最近的簇中（E），重新计算簇的质心作为新的质心使损失函数式(9.24)最小化（M）。因此，k-means具有EM算法的所有缺点，并且仅适合发现类圆形状的簇。
模型训练
代码地址 https://github.com/qianshuang/ml-exp
from sklearn.cluster import KMeans
from data.cnews_loader import *
base_dir = 'data/cnews'
test_dir = os.path.join(base_dir, 'cnews.kmeans.test.txt')
vocab_dir = os.path.join(base_dir, 'cnews.kmeans.vocab.txt')
if not os.path.exists(vocab_dir):
# 构建词典表
build_vocab(test_dir, vocab_dir)
categories, cat_to_id = read_category()
words, word_to_id = read_vocab(vocab_dir)
print("start doing k-means...")
# 处理数据
feature, target = process_file(test_dir, word_to_id, cat_to_id)
# 训练k-means聚类
kmeans = KMeans(n_clusters=10, random_state=0).fit(feature) # random_state为随机数种子，若不设置每次运行结果不一样
print(kmeans.predict([feature[0]])) # 预测簇id
print(kmeans.cluster_centers_) # 聚类中心
print(kmeans.labels_) # 返回所有簇id
print(metrics.calinski_harabaz_score(feature, kmeans.predict(feature))) # Calinski-Harabasz分数可以用来评估聚类效果，它内部使用簇内的稠密程度和簇间的离散程度的比值，所以数值越大效果越好
运行结果：
read_category...
read_vocab...
start doing k-means...
[5]
[[ 1.58536585e-01 1.70731707e-01 1.95121951e-01 ... 8.53658537e-02
8.53658537e-02 3.65853659e-02]
[ 1.66533454e-16 4.05405405e-02 3.24324324e-01 ... 4.05405405e-02
1.52655666e-16 1.73472348e-17]
[ 2.02702703e-01 1.80180180e-02 1.44144144e-01 ... 3.15315315e-02
4.95495495e-02 -4.85722573e-17]
...
[ 1.75675676e-01 1.35135135e-02 6.89189189e-01 ... -4.16333634e-17
1.08108108e-01 1.73472348e-17]
[ 1.26760563e-01 4.22535211e-02 2.11267606e-01 ... 1.40845070e-02
1.52655666e-16 1.38777878e-17]
[ 7.14285714e-01 2.85714286e-01 5.71428571e-01 ... 6.93889390e-18
4.28571429e-01 0.00000000e+00]]
[5 0 6 4 6 5 2 4 1 1 3 4 7 4 2 7 8 2 1 3 2 4 7 2 3 6 5 8 2 3 5 2 6 6 7 3 3
6 7 3 3 4 4 5 4 7 2 4 2 1 0 0 2 0 5 4 6 8 6 7 3 2 2 6 2 6 4 2 7 6 2 2 2 6
2 0 7 6 2 8 5 0 0 6 5 6 4 4 5 6 1 5 6 7 1 8 8 2 4 3 4 3 2 6 8 0 8 2 3 6 2
4 6 2 9 6 2 0 4 4 5 0 2 3 5 8 2 6 2 0 1 3 0 2 6 7 3 0 6 1 7 6 0 1 2 4 3 3
2 2 2 2 6 2 3 9 6 8 0 7 3 1 4 2 4 2 4 7 4 6 7 6 4 3 6 2 6 2 0 3 8 2 4 5 3
4 6 3 6 7 2 4 4 7 4 6 5 1 4 3 8 2 3 6 4 2 7 4 5 2 1 8 2 1 4 4 0 6 4 3 4 2
4 8 6 7 0 5 7 5 0 8 3 7 2 2 3 0 0 5 6 6 4 2 0 1 6 4 6 2 5 2 7 0 2 3 1 3 2
5 2 8 6 0 3 2 2 2 2 3 4 6 4 3 3 4 1 2 2 3 6 4 2 5 4 6 2 4 0 7 7 6 6 2 4 0
5 7 5 2 6 2 6 5 7 4 1 7 5 2 2 2 4 8 8 7 2 4 2 6 2 2 4 6 2 3 5 8 5 3 0 1 4
2 2 2 7 7 4 3 3 5 1 3 2 2 8 3 3 2 7 8 3 4 0 2 6 2 4 3 6 6 1 3 4 5 5 7 7 0
3 5 5 1 4 5 2 4 1 8 2 5 4 8 2 1 5 4 2 0 3 4 7 1 2 8 8 2 6 7 8 1 2 4 2 2 4
5 5 5 3 5 2 8 6 2 2 6 0 6 1 6 6 4 5 2 7 7 2 8 4 4 3 6 5 0 0 4 5 3 2 4 6 1
6 2 5 6 6 4 0 1 8 2 8 7 3 2 1 2 4 4 4 5 5 6 6 5 8 8 6 5 2 8 5 2 5 5 6 4 1
3 4 7 2 2 2 7 2 1 7 3 2 3 2 7 5 4 4 3 1 4 7 3 8 0 5 4 8 2 7 3 1 6 6 5 7 2
8 1 8 0 1 0 4 0 4 6 2 5 2 4 1 4 7 3 1 3 2 8 8 8 2 2 4 0 6 2 3 4 4 6 0 3 3
1 2 4 0 2 4 7 3 3 4 8 2 0 2 4 2 4 4 5 5 4 0 4 5 4 2 5 1 1 2 2 8 0 5 4 5 5
3 4 8 5 0 8 8 3 7 6 4 6 0 5 1 2 3 2 6 5 7 3 6 0 1 2 0 3 0 8 1 3 2 3 0 1 7
6 5 2 5 8 3 3 6 8 2 2 6 3 2 6 3 2 1 8 5 6 3 8 7 4 6 0 8 6 2 8 3 2 0 4 4 1
2 0 6 4 2 0 3 1 2 1 0 2 5 3 4 3 3 1 0 4 7 6 8 3 2 6 2 5 3 5 8 2 2 1 3 1 4
7 7 4 2 8 3 2 7 2 8 1 2 4 6 5 1 3 7 0 2 1 4 8 3 4 8 0 8 2 3 6 7 2 2 4 2 6
5 0 0 5 0 2 5 6 5 5 0 2 7 5 1 5 0 5 7 6 2 5 8 3 2 6 9 3 0 4 5 1 2 6 5 0 2
1 6 0 2 2 6 8 5 1 3 3 3 3 2 1 1 2 9 1 2 3 5 2 5 0 2 2 7 0 5 4 0 1 7 4 7 2
5 7 1 2 2 6 3 0 5 3 2 7 4 5 0 6 8 3 3 2 4 2 7 5 9 2 2 7 2 8 2 2 2 1 2 0 4
2 3 7 2 6 6 9 2 0 4 4 4 5 6 1 6 6 3 2 9 4 8 0 8 3 2 2 0 2 2 3 6 2 4 7 4 2
5 0 3 6 3 6 2 3 2 0 5 3 2 5 2 3 1 0 3 4 2 6 2 8 5 6 3 2 5 0 4 7 2 2 2 1 5
2 8 2 3 2 1 5 2 3 4 7 1 2 8 3 2 2 2 2 4 6 5 5 8 4 2 3 4 7 2 8 7 2 8 5 0 6
2 3 4 6 2 2 6 0 3 4 5 3 1 3 2 2 7 4 2 1 3 1 2 6 1 7 2 2 0 4 6 1 6 5 2 5 4
2]
18.01038055734191
社群
- QQ交流群
- 微信交流群
- 微信公众号
