算法原理
GAN,生成对抗网络,该模型主要包含两个核心模块:一个是判别器,一个是生成器。比如,我们有一批真实数据,同时也有一批随机生成的假数据,生成器A拼命地把随手拿过来的假数据模仿成真实数据,并揉进真实数据里,判别器B则拼命地想把真实数据和假数据区分开。A类似于造假币的,B类似于稽查警察,A一个劲地学习如何骗过B,而B则是一个劲地学习如何分辨出A的造假技巧。如此这般,随着B的鉴别技巧的越来越厉害,A的造假技巧也是越来越纯熟,而一个一流的假币制造者就是我们所需要的。这就是GAN背后的思想,十分的直观与朴素。
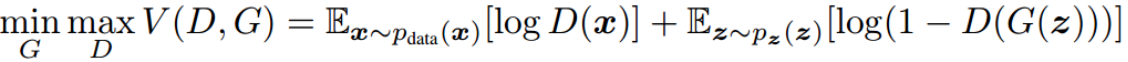
- GAN的目标是令生成器生成与真实数据几乎没有区别的样本,数学上来讲即将随机变量生成为某一种概率分布,该分布的概率密度函数等于真实数据的概率密度函数,即P_G(x)=P_data(x)。为了学习到生成器G在数据X上的分布P_G,我们先定义一个先验的输入噪声变量z,然后根据G(z)将其映射到数据空间X中,然后再定义一个判别器D,它的输出为单个标量。D(x)表示x来源于真实数据而不是P_G的概率。
- E指取期望,其实也就是极大似然估计,最大化加号前一项相当于令判别器D在X服从data的概率密度时能准确地预测D(x)=1,对于D而言要尽量使价值函数V(D,G)最大化(识别能力强),而对于G而言,又想使之最小(生成的数据接近实际数据)。
- 整个训练是一个不断迭代的过程,即在给定G的情况下先最大化V(D,G)而训练D,当D有了一定的辨别能力后,固定D,然后最小化V(D,G)而训练G。
- 迭代的固定其中一个,训练另一个(一般D训练K步后才训练G一次),最终模型会到达一个均衡点,这个时候生成器的概率密度函数等于真实数据的概率密度函数,也即生成的数据和真实数据是一样的,在均衡点上D和G都不能得到进一步提升,并且判别器无法判断数据到底是来自真实样本还是伪造的数据,即D(x)=1/2。
总地来说,GAN是通过对抗过程估计生成模型的新框架。即我们需要同时训练两个模型,一个能捕获数据分布的生成模型G和一个能估计数据来源于真实样本概率的判别模型D。生成器G的训练过程是最大化判别器犯错误的概率,即判别器误以为数据是真实样本而不是生成器生成的假样本。因此,这一框架就对应于两个参与者的极小极大博弈(minimax game)。在所有可能的函数G和D中,我们可以求出唯一均衡解,即G可以生成与训练样本相同的分布,而D判断的概率处处为1/2。
代码实现
# 定义判别器
D_W1 = tf.Variable(variable_init([784, 128]))
D_b1 = tf.Variable(tf.zeros(shape=[128]))
D_W2 = tf.Variable(variable_init([128, 1]))
D_b2 = tf.Variable(tf.zeros(shape=[1]))
theta_D = [D_W1, D_W2, D_b1, D_b2]
def discriminator(x):
D_h1 = tf.nn.relu(tf.matmul(x, D_W1) + D_b1)
D_logit = tf.matmul(D_h1, D_W2) + D_b2
# 即判别输入的图像到底是真(1)还是假(0)
D_prob = tf.nn.sigmoid(D_logit)
return D_prob, D_logit
# 定义生成器
G_W1 = tf.Variable(variable_init([100, 128]))
G_b1 = tf.Variable(tf.zeros(shape=[128]))
G_W2 = tf.Variable(variable_init([128, 784]))
G_b2 = tf.Variable(tf.zeros(shape=[784]))
theta_G = [G_W1, G_W2, G_b1, G_b2]
def generator(z):
G_h1 = tf.nn.relu(tf.matmul(z, G_W1) + G_b1)
G_log_prob = tf.matmul(G_h1, G_W2) + G_b2
G_prob = tf.nn.sigmoid(G_log_prob)
# 输出784维的向量,reshape为28×28后就是一张图像
return G_prob
# 构建模型graph
Z = tf.placeholder(tf.float32, shape=[None, 100]) # 生成器的输入噪声,100维向量
X = tf.placeholder(tf.float32, shape=[None, 784]) # 输入的真实图片
G_sample = generator(Z) # 生成fake图片
D_real, D_logit_real = discriminator(X) # 输入真实图片,判断真伪
D_fake, D_logit_fake = discriminator(G_sample) # 输入fake图片,判断真伪
# 以下为原论文的判别器损失和生成器损失
# D_loss = -tf.reduce_mean(tf.log(D_real) + tf.log(1. - D_fake))
# G_loss = -tf.reduce_mean(tf.log(D_fake))
# 判别器判别真实图片的结果要尽量接近全1,E[log(D(x))]
D_loss_real = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_logit_real, labels=tf.ones_like(D_logit_real)))
# 判别器判别生成图片的结果要尽量接近全0,E[log(1-D(G(z)))]
D_loss_fake = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_logit_fake, labels=tf.zeros_like(D_logit_fake)))
D_loss = D_loss_real + D_loss_fake
# 对于生成器loss,判别器判别生成图片的结果要尽量接近全1,E[log(1-D(G(z)))]
G_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_logit_fake, labels=tf.ones_like(D_logit_fake)))
# 判别器和生成器分开做迭代优化(固定参数)
D_solver = tf.train.AdamOptimizer().minimize(D_loss, var_list=theta_D)
G_solver = tf.train.AdamOptimizer().minimize(G_loss, var_list=theta_G)
# 模型训练
sess = tf.Session()
sess.run(tf.global_variables_initializer())
for it in range(20000):
# 每2000次迭代输出一张生成器生成的图片
if it % 2000 == 0:
samples = sess.run(G_sample, feed_dict={Z: sample_Z(16, Z_dim)})
fig = plot(samples)
plt.savefig('out/{}.png'.format(str(i).zfill(3)), bbox_inches='tight')
plt.close(fig)
# 随机抽取128张真实图片
X_mb, _ = mnist.train.next_batch(128)
_, D_loss_curr = sess.run([D_solver, D_loss], feed_dict={X: X_mb, Z: np.random.uniform(-1., 1., size=[128, 100])})
_, G_loss_curr = sess.run([G_solver, G_loss], feed_dict={Z: np.random.uniform(-1., 1., size=[128, 100])})
# 每迭代2000次输出迭代数、生成器损失和判别器损失
if it % 2000 == 0:
print('Iter: {}'.format(it))
print('D loss: {:.4}'. format(D_loss_curr))
print('G_loss: {:.4}'.format(G_loss_curr))
print()
社群
- QQ交流群

- 微信交流群

- 微信公众号
