深度学习 强化学习 reinforcement learning

32.0 强化学习

Posted by 子颢 on September 4, 2018

算法原理

强化学习其实是独立于机器学习和深度学习的一门学科，既不属于有监督学习，也不属于无监督学习。在强化学习中，智能体（agent）在环境（environment）中进行观察（observe）并采取行动（action），它会收到奖励（reward）作为回报。其目标是学会以最大化其预期的长期奖励（long-term rewards）行事。 agent用来确定其action的算法称为其策略（policy）。例如该policy可以是将观察observation作为输入并输出要采取的动作action的神经网络。通过评估rewards关于policy参数的梯度，然后通过梯度上升（使rewards最大化）来调整这些参数，这就是policy gradients强化学习算法。 but，强化学习的训练很多时候是很不稳定的，并且算法本身存在高方差，难优化等问题，还有强化学习的reward的设计，环境建模，也是比较大的问题。

OpenAI Gym

OpenAI gym是一个提供各种强化学习模拟环境的工具包，你可以用它来训练、开发并试验新的强化学习（RL）算法。 其安装非常简单：

pip3 install --upgrade gym

让我们从RL的hello world程序——平衡车（CartPole）入手，一点点深入强化学习的大门。 RL

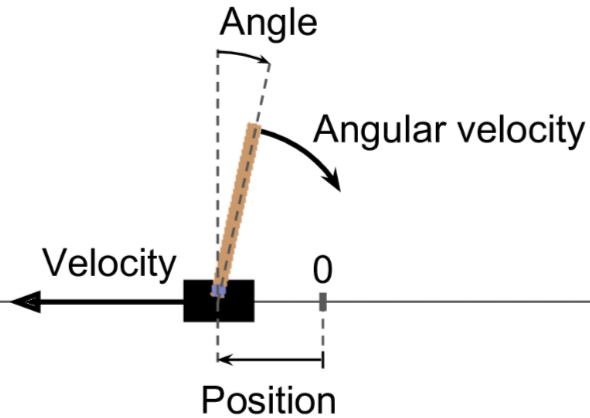
# 创建一个CartPole的环境模拟器，可以向左或向右加速推车，以平衡放置在其顶部的杆
env = gym.make("CartPole-v0")
# 初始化环境变量，返回第一个观察结果
obs = env.reset()
# 每个值的含义分别是：小车的水平位置(0.0 = center)、速度、杆的角度(0.0 = 垂直)、杆的角速度
print(obs)  # [-0.03446547 -0.04519292  0.01626575 -0.01777462]
# 渲染并显示环境
env.render()

# 可能采取的行动只能是两个离散的值，向左(0)和向右(1)
print(env.action_space)  # Discrete(2)
# step表示执行一步动作，这里向右移动一步
action = 1
obs, reward, done, info = env.step(action)
# 采取行动后的下一个观测结果：向右为+，向左为-
print(obs)  # [ 0.01969743  0.23745748 -0.02107486 -0.26251706]
# 采取行动后的奖励，不管采取什么动作，奖励都是1，所以我们的目标是尽量让小车运行的时间长，实际中奖励值根据先验知识确定，并且越丰富越好
print(reward)  # 1.0
# 当执行完所有episode后才会返回True。当小车倾斜角度太大，或者小车跑出屏幕，游戏结束也会返回True，这时环境必须reset才能重用
print(done)  # False
# debug信息
print(info)  # {}

basic policy

我们首先使用一个最基本的硬编码的策略，即杆向左倾斜时向左走，向右倾斜时向右走，我们来看下小车最长能坚持多久（得到多少奖励）。

import gym
import numpy as np

env = gym.make("CartPole-v0")


# 杆向左倾斜时向左走，向右倾斜时向右走
def basic_policy(obs):
    angle = obs[2]
    return 0 if angle < 0 else 1


totals = [1,2,3]
for episode in range(50):
    episode_rewards = 0
    obs = env.reset()
    for step in range(100):  # 100 steps max, we don't want to run forever
        action = basic_policy(obs)
        obs, reward, done, info = env.step(action)
        env.render()
        episode_rewards += reward
        if done:
            break
    totals.append(episode_rewards)

print(np.mean(totals), np.std(totals), np.min(totals), np.max(totals))  # 41.132075471698116 12.619298990560923 1.0 64.0

可以看到：

Neural Network Policy

我们现在用Neural Network Policy代替Basic Policy，这时候我们的输入不再是obs[2]这一个环境变量，而是所有的4个环境变量值，我们输出每一个action的概率，由于只有两种action，所以我们只需要一个输出神经元代表action取0即向左走的概率。注意这时候我们并不是取得分最高的action，而是根据神经网络输出的概率值来选择action，这种方法可以让智能体在探索新路径和利用已知运行良好的路径之间找到适当的平衡点，即让智能体具有一定的全局观，因为我们的目的是希望最大化长期奖励，而不是目光短浅的每次都取当前最高得分的action。 RL

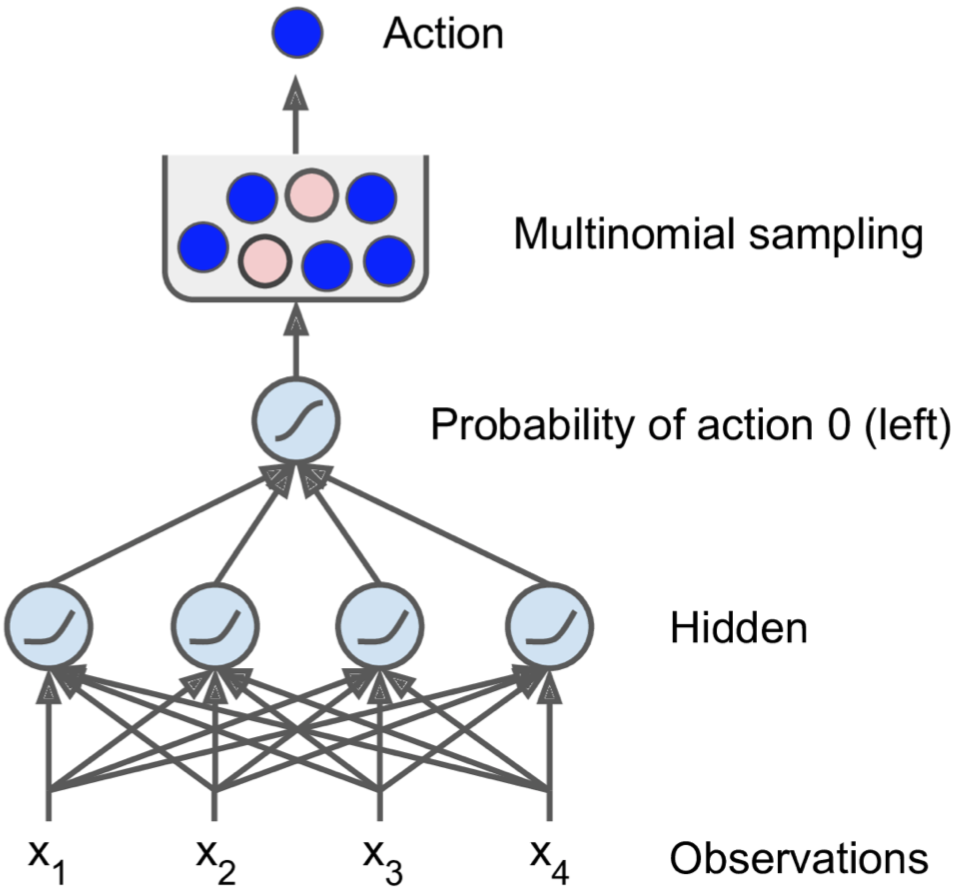
n_inputs = 4  # 使用所有的环境变量值
n_hidden = 4  # it's a simple task, we don't need more hidden neurons
n_outputs = 1  # only outputs the probability of accelerating left
initializer = tf.contrib.layers.variance_scaling_initializer()

X = tf.placeholder(tf.float32, shape=[None, n_inputs])
hidden = fully_connected(X, n_hidden, activation_fn=tf.nn.elu, weights_initializer=initializer)
logits = fully_connected(hidden, n_outputs, activation_fn=None, weights_initializer=initializer)
outputs = tf.nn.sigmoid(logits)
# Select a random action based on the estimated probabilities
p_left_and_right = tf.concat(axis=1, values=[outputs, 1 - outputs])
# 如果用数组[np.log(0.5), np.log(0.2), np.log(0.3)]，并且num_samples=5，那么该函数将输出5个整数，每个整数以50%概率取0，20%概率取1，30%概率取2
action = tf.multinomial(tf.log(p_left_and_right), num_samples=1)
return action

Evaluating Actions

在我们的平衡车问题中，每一个step的action都会产生一个reward，并且这个reward恒为1，也就是所有action效果一样，但是我们知道每一个step的action的效果有好有坏，比如可能这一步走了一把好棋，直接奠定了胜利的基础，也可能走了一步怀棋，直接埋下了祸根，所以每一个step的action都对以后产生了深远的影响，因此每一个step的action应该有一个score值，用这个score值来衡量这一步action的好坏程度，这个score怎么得来呢？因为每一步的action都对未来的action产生了影响，所以未来的action得到的rewards理应贡献一部分给当前step的action，而且距离越远衰减越厉害（影响越小）。我们可以使用一个超参数discount rate作为衰减系数，一般取值为0.95或0.99。 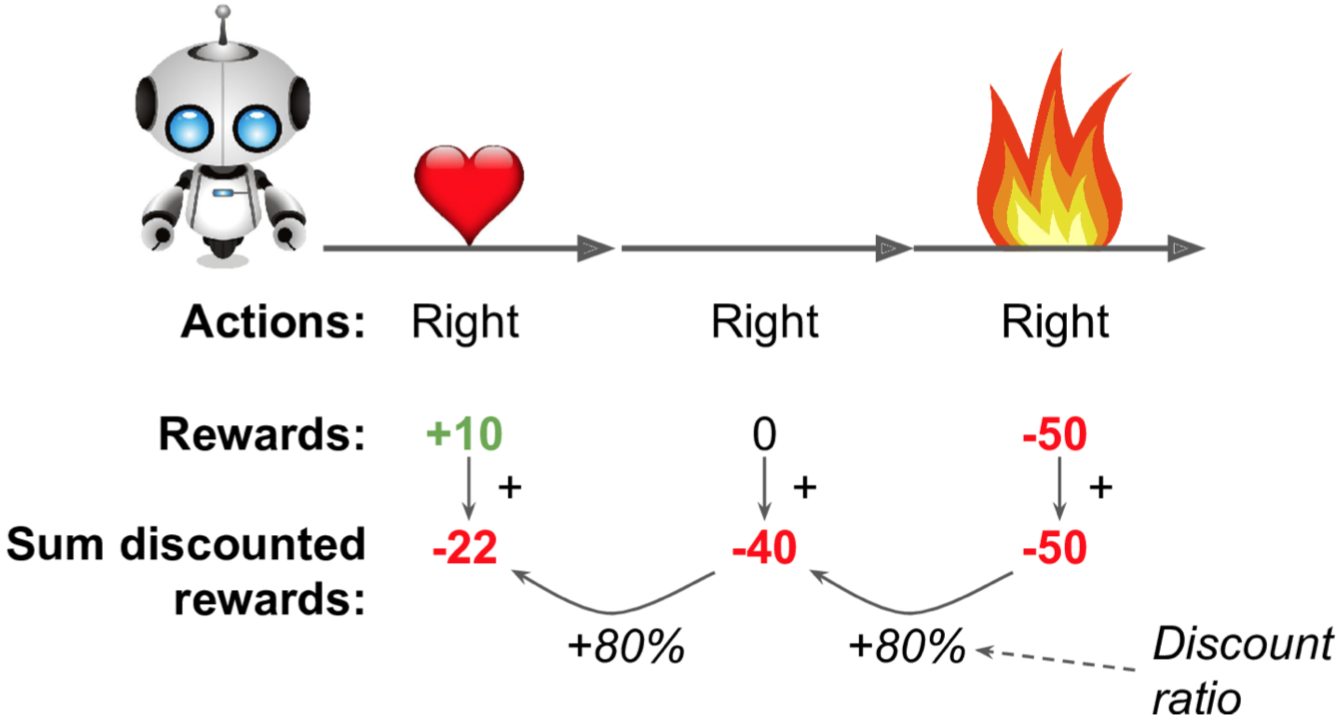RL 假如现在一个智能体往右走了三步游戏就结束了，分别得到了+10、0、-50的rewards，我们使用discount rate r = 0.8，那么第一个step的action的score值为：10 + r×0 + r^2 × (–50) = –22。当然一个好的action的score可能会由于后面连接了几个坏的action而拉低了分值（猪队友），但是不用担心，只要玩的足够多次，最终来说好的action的score会高于坏的action，为了得到更加可信的score，最后可能还需要对score进行标准化，这样我们就有理由认为负分代表bad actions，正分代表good actions，并且分值越高，action越好。

Policy Gradients with Gradients*aciton_scores form

前面说到，通过评估rewards关于policy参数的梯度，然后通过梯度上升（使rewards最大化）来调整这些参数，这就是policy gradients强化学习算法。也即我们的NN policy的参数训练过程。policy gradients具体算法步骤如下：

  1. 使用neural network policy玩游戏多次，并且在每一步计算action的梯度（仅计算，并不apply gradients）。
  2. 使用discount rate方法计算每一步的action的score。
  3. 如果某个action的score为正，则表示该action是好的，并且我们希望应用之前计算的gradients以使该动作更有可能在将来被选中(梯度下降)。如果score为负，则表示该action很糟糕，并且我们希望应用相反的gradients来使此action在将来稍微不太可能被选中（梯度上升）。解决方案非常简单而且巧妙，直接将每个梯度向量乘以相应的action score。
  4. 最后，计算所有得到的梯度向量的平均值，并使用它来执行梯度下降步骤。

下面我们一起来看下TensorFlow的实现过程，首先构建计算图：

class TextCNN(object):
    def __init__(self, config):
        self.config = config

        self.input_x = tf.placeholder(tf.float32, [None, self.config.n_inputs], name='input_x')
        self.policy_gradients()

    def policy_gradients(self):
        initializer = tf.contrib.layers.variance_scaling_initializer()
        hidden = tf.contrib.layers.fully_connected(self.input_x, 4, activation_fn=tf.nn.elu, weights_initializer=initializer)
        logits = tf.contrib.layers.fully_connected(hidden, self.config.n_outputs, activation_fn=None, weights_initializer=initializer)
        outputs = tf.nn.sigmoid(logits)
        # 计算向左和向右的概率
        p_left_and_right = tf.concat([outputs, 1 - outputs], axis=1)
        # 根据概率采样action
        self.action = tf.multinomial(tf.log(p_left_and_right), num_samples=1)
        # the target probability must be 1.0 if the chosen action is action 0 (left) and 0.0 if it is action 1 (right)
        y = 1. - tf.to_float(self.action)
        # 我们认为选择的action就是最好的action，效果就是让rewards最大化
        cross_entropy = tf.nn.sigmoid_cross_entropy_with_logits(labels=y, logits=logits)
        self.loss = tf.reduce_mean(cross_entropy)
        # 计算梯度
        optimizer = tf.train.AdamOptimizer(self.config.learning_rate)
        grads_and_vars = optimizer.compute_gradients(cross_entropy)
        self.gradients = [grad for grad, variable in grads_and_vars]
        self.gradient_placeholders = []
        grads_and_vars_feed = []
        for grad, variable in grads_and_vars:  # variable是NN policy的参数矩阵W和b（作为整体）的变量名
            # gradient_placeholder用来传入调整后的梯度值，即gradients * action_score->标准化->平均后的新的梯度值
            gradient_placeholder = tf.placeholder(tf.float32, shape=grad.get_shape())
            # Tensor("Placeholder:0", shape=(4, 4), dtype=float32)
            # Tensor("Placeholder_1:0", shape=(4,), dtype=float32)
            # Tensor("Placeholder_2:0", shape=(4, 1), dtype=float32)
            # Tensor("Placeholder_3:0", shape=(1,), dtype=float32)
            print(gradient_placeholder)  # 同grad的shape
            self.gradient_placeholders.append(gradient_placeholder)
            # 将调整后的梯度值feed给优化器，以执行优化
            grads_and_vars_feed.append((gradient_placeholder, variable))
        self.training_op = optimizer.apply_gradients(grads_and_vars_feed)

模型训练：

for iteration in range(config.n_iterations):
    all_rewards = []  # all sequences of raw rewards for each episode
    all_gradients = []  # gradients saved at each step of each episode
    all_loss = []
    for game in range(config.n_games_per_update):
        current_rewards = []  # all raw rewards from the current episode
        current_gradients = []  # all gradients from the current episode
        current_loss = []

        obs = env.reset()
        for step in range(config.n_max_steps):
            action_val, gradients_val, loss_val = sess.run(
                [model.action, model.gradients, model.loss],
                feed_dict={model.input_x: obs.reshape(1, config.n_inputs)})  # one obs
            obs, reward, done, info = env.step(action_val[0][0])
            # env.render()  # render方法比较耗时
            current_rewards.append(reward)
            current_gradients.append(gradients_val)
            current_loss.append(loss_val)

            if done:
                break
        all_rewards.append(current_rewards)
        all_gradients.append(current_gradients)
        all_loss.append(current_loss)

    # At this point we have run the policy for 10 episodes, and we are ready for a policy update using the algorithm described earlier.
    all_rewards_discount = discount_and_normalize_rewards(all_rewards, config.discount_rate)
    feed_dict = {}
    for var_index, grad_placeholder in enumerate(model.gradient_placeholders):
        # multiply the gradients by the action scores, and compute the mean
        compute_gradients = []  # W1:[n_games_per_update, 4, 4] b1:[n_games_per_update, 4] W2:[n_games_per_update, 4, 1] b2:[n_games_per_update, 1]
        for game_index, rewards in enumerate(all_rewards_discount):
            for step, reward in enumerate(rewards):
                compute_gradient = reward * all_gradients[game_index][step][var_index]
                compute_gradients.append(compute_gradient)
        mean_gradients = np.mean(compute_gradients, axis=0)  # 按位取平均
        # 下面是一步到位的写法，可读性较差
        # mean_gradients = np.mean(
        #     [reward * all_gradients[game_index][step][var_index]
        #      for game_index, rewards in enumerate(all_rewards)
        #      for step, reward in enumerate(rewards)],
        #     axis=0)
        # print(mean_gradients)
        feed_dict[grad_placeholder] = mean_gradients
    sess.run(model.training_op, feed_dict=feed_dict)

Policy Gradients with loss*aciton_scores form

下面的方法在上面的基础上稍加简化，每一个epoch训练一次，并且通过action_score的正负向来指导neg_log_prob，与通过action_score的正负向来指导梯度更新是一样的效果。
构建计算图：

class TextCNN(object):
    def __init__(self, config):
        self.config = config

        self.input_x = tf.placeholder(tf.float32, [None, self.config.n_inputs], name='input_x')
        self.input_actions = tf.placeholder(tf.int32, [None, ], name='input_actions')
        self.input_action_scores = tf.placeholder(tf.float32, [None, ], name="input_action_scores")
        self.policy_gradients()

    def policy_gradients(self):
        initializer = tf.contrib.layers.variance_scaling_initializer()
        hidden = tf.contrib.layers.fully_connected(self.input_x, 4, activation_fn=tf.nn.elu, weights_initializer=initializer)
        logits = tf.contrib.layers.fully_connected(hidden, self.config.n_outputs, activation_fn=None, weights_initializer=initializer)
        self.outputs = tf.nn.softmax(logits)

        # 我们认为选择的action就是最好的action
        neg_log_prob = tf.reduce_sum(-tf.log(self.outputs) * tf.one_hot(self.input_actions, self.config.n_outputs), axis=1)
        # 或者是用下面的方式，两种方式等价
        # neg_log_prob = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=logits, labels=self.input_actions)
        # reward guided loss，这里通过action_score的正负向来指导neg_log_prob，与通过action_score的正负向来指导梯度更新是一样的效果
        self.loss = tf.reduce_mean(neg_log_prob * self.input_action_scores)
        self.train_op = tf.train.AdamOptimizer(self.config.learning_rate).minimize(self.loss)

模型训练：

for iteration in range(config.n_iterations):
    all_rewards = []  # all raw rewards from the current episode
    all_actions = []
    all_inputs = []

    obs = env.reset()

    while True:
        inputs = obs.reshape(1, config.n_inputs)
        action_prob = sess.run(
            [model.outputs],
            feed_dict={model.input_x: inputs})  # one obs
        a = [i for i in range(len(np.array(action_prob).ravel()))]
        p = np.array(action_prob).ravel()
        action = np.random.choice(a, p=p)
        obs_, reward, done, info = env.step(action)
        # env.render()  # render方法比较耗时
        all_rewards.append(reward)
        all_actions.append(action)
        all_inputs.append(inputs)

        if done:
            # 每一个epoch都进行训练
            discounted_ep_rs_norm = discount_and_normalize_rewards([all_rewards], config.discount_rate)[0]
            # train on episode
            loss, _ = sess.run([model.loss, model.train_op], feed_dict={
                model.input_x: np.vstack(all_inputs),
                model.input_actions: all_actions,  # shape=[None, ]
                model.input_action_scores: discounted_ep_rs_norm,  # shape=[None, ]
            })

            break

        obs = obs_

马尔科夫决策过程

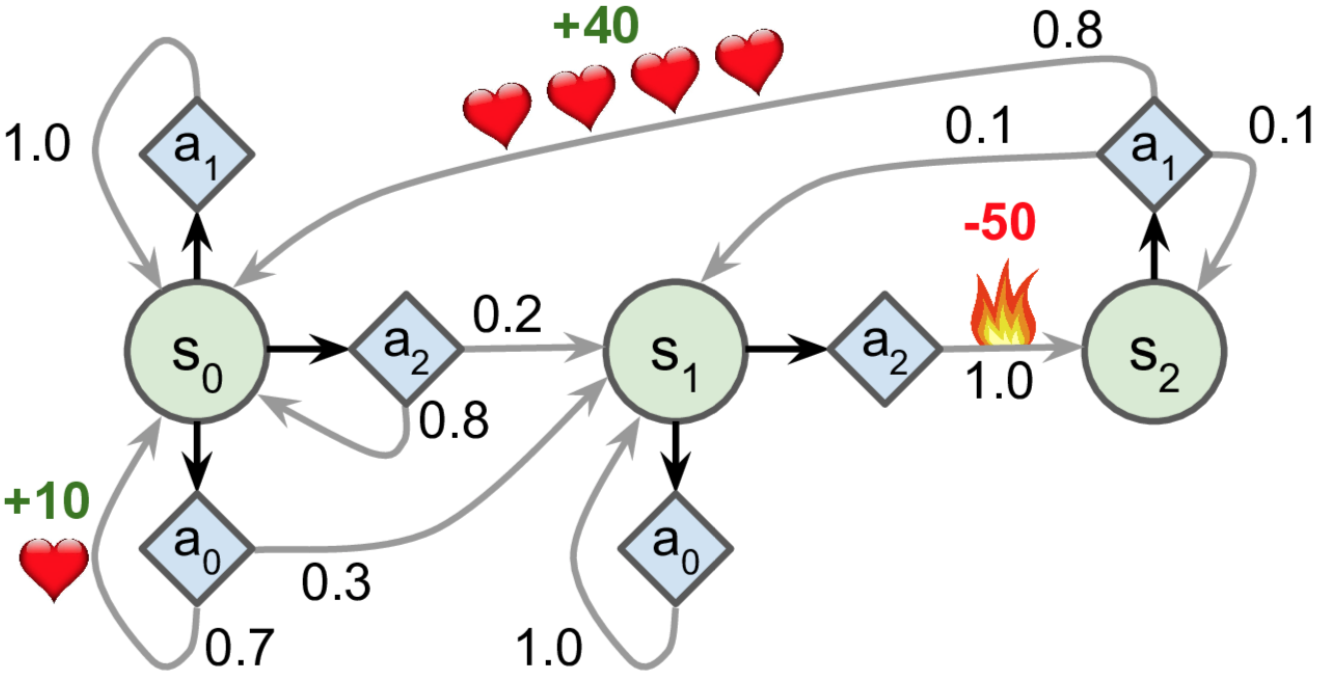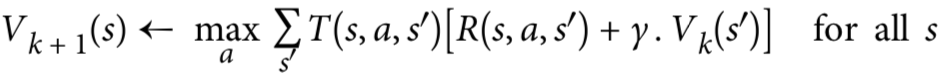
马尔科夫决策过程（Markov Decision Processes，MDP），即在马尔科夫网络的基础上加入了动作（action）和奖励（rewards）。 RL MDP要解决的关键问题是估计每一状态的最佳状态值，这是一个迭代的过程，因为在某一状态执行每一动作之后会对未来产生深远的影响，所以未来的每一状态得到的rewards理应贡献一部分给当前状态，而且距离越远衰减越厉害。所以每一状态的最佳状态值可以通过以下公式计算： RL RL 首先可以将所有状态估计值初始化为零，然后使用该算法迭代更新它们，只要给定足够的时间，这些估计值可以保证收敛到最佳状态值。

知道了每一状态的最佳状态值并没有明确告诉智能体应该在每一状态采取什么动作，所以我们在上面公式的基础上稍加修改，就可以得到state-action pair (s,a)的最优值，即Q-Values，这个Q-Values就是模型要学习的东西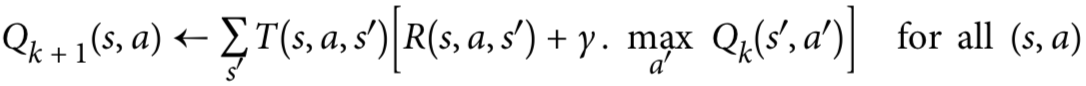： RL 一旦获得了最佳Q值，定义最优策略就简单了，当agent处于状态s时，它应该始终选择具有最高Q值的动作。 下面我们通过程序模拟以下MDP：

nan = np.nan  # represents impossible actions
# shape=[s, a, s'], 即[3, 3, 3]，比如第2行第1列的[0.0, 1.0, 0.0]代表s1a0s0,s1a0s1,s1a0s2
T = np.array([
    [[0.7, 0.3, 0.0], [1.0, 0.0, 0.0], [0.8, 0.2, 0.0]],
    [[0.0, 1.0, 0.0], [nan, nan, nan], [0.0, 0.0, 1.0]],
    [[nan, nan, nan], [0.8, 0.1, 0.1], [nan, nan, nan]],
])
R = np.array([  # shape=[s, a, s']
    [[10., 0.0, 0.0], [0.0, 0.0, 0.0], [0.0, 0.0, 0.0]],
    [[10., 0.0, 0.0], [nan, nan, nan], [0.0, 0.0, -50.]],
    [[nan, nan, nan], [40., 0.0, 0.0], [nan, nan, nan]],
])
# 每个状态可能采取的action
possible_actions = [[0, 1, 2], [0, 2], [1]]
# -inf for impossible actions
Q = np.full((3, 3), -np.inf)
# Initial value = 0.0, for all possible actions
for state, actions in enumerate(possible_actions):
    Q[state, actions] = 0.0
# learning_rate = 0.01
discount_rate = 0.95
n_iterations = 100
for iteration in range(n_iterations):
    Q_prev = Q.copy()
    for s in range(3):
        for a in possible_actions[s]:
            Q[s, a] = np.sum([
                T[s, a, sp] * (R[s, a, sp] + discount_rate * np.max(Q_prev[sp]))
                for sp in range(3)
            ])

print(Q)  # [[21.88646117 20.79149867 16.854807], [1.10804034 -inf 1.16703135], [-inf 53.8607061 -inf]]，最终趋于稳定
print(np.argmax(Q, axis=1))  # [0 2 1]，optimal action for each state

Q-learning

对于强化学习来说，上面的T矩阵与R矩阵我们事先并不可知，agent必须经历每个state和每个transition至少一次以了解奖励，并且如果要对转移矩阵进行合理估计，它必须经历多次。所以agent需要使用探索策略（例如纯随机策略）来探索MDP，并且随着每次不同的探索，agent根据实际观察到的transition和rewards更新状态值的估计值。再继续在MDP算法的基础上稍加改动就得到了我们的Q-learning算法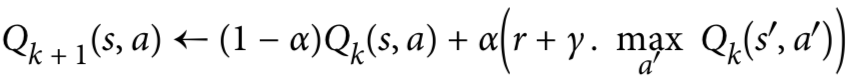： RL α是学习率，r是reward，γ是discount rate，对于每个（s，a）pair，Q-learning算法跟踪agent在离开具有动作a的状态s时获得的奖励的运行平均值，以及它期望稍后获得的奖励。下面还是通过代码实现Q-learning算法：

learning_rate0 = 0.05
learning_rate_decay = 0.1
discount_rate = 0.95
n_iterations = 20000

s = 0  # start in state 0
Q = np.full((3, 3), -np.inf) # -inf for impossible actions
possible_actions = [[0, 1, 2], [0, 2], [1]]
for state, actions in enumerate(possible_actions):
    Q[state, actions] = 0.0 # Initial value = 0.0, for all possible actions

for iteration in range(n_iterations):
    a = rnd.choice(possible_actions[s])  # choose an action (randomly)
    sp = rnd.choice(range(3), p=T[s, a])  # pick next state using T[s, a]
    reward = R[s, a, sp]  # 跟踪agent在离开具有动作a的状态s时获得的奖励的运行平均值
    learning_rate = learning_rate0 / (1 + iteration * learning_rate_decay)
    Q[s, a] = learning_rate * Q[s, a] + (1 - learning_rate) * (reward + discount_rate * np.max(Q[sp]))
    s = sp  # move to next state

当迭代次数足够多时，该算法将收敛得到最佳的Q值。

模型训练

代码地址 https://github.com/qianshuang/rl_exp

运行结果：

Configuring model...
Tensor("Placeholder:0", shape=(4, 4), dtype=float32)
Tensor("Placeholder_1:0", shape=(4,), dtype=float32)
Tensor("Placeholder_2:0", shape=(4, 1), dtype=float32)
Tensor("Placeholder_3:0", shape=(1,), dtype=float32)
Training and evaluating...
Iter:      1, Train Loss:   0.65, Avg Steps:   15.5,Time: 0:00:00
Iter:      2, Train Loss:   0.69, Avg Steps:   15.3,Time: 0:00:00
Iter:      3, Train Loss:   0.68, Avg Steps:   18.5,Time: 0:00:01
Iter:      4, Train Loss:   0.67, Avg Steps:   23.3,Time: 0:00:01
······
······
Iter:     98, Train Loss:    0.6, Avg Steps:  149.4,Time: 0:01:34
Iter:     99, Train Loss:    0.6, Avg Steps:  148.8,Time: 0:01:35
Iter:    100, Train Loss:   0.59, Avg Steps:  186.3,Time: 0:01:37

社群

CATALOG
    FEATURED TAGS
    机器学习 模型部署 在线预测 推荐系统 深度学习 TensorFlow 迁移学习 seq2seq 机器翻译 GPU 知识图谱 Knowledge Graph KG 计算机视觉 computer vision CV OCR 目标检测 NLP 语音识别 chatGPT

    分享到: 微博 微信

    返回顶部