时光飞逝，岁月如梭，距离上一篇POST已经过去了一年半的时间，这段时间主要是处理公司的事情以及沉淀自我。废话不多说，今天主要想带着大家深刻理解一下transformer模型架构，并且用我们之前的文本分类案例来实战transformer模型。
模型架构
Transformer模型出自于Google在2017年的一篇论文《Attention Is All You Need》，Google将Transformer模型应用到机器翻译任务上，显著提升了该任务的效果和效率，我们之前讲到的BERT，其核心也是transformer模型。transformer模型架构如下图所示：
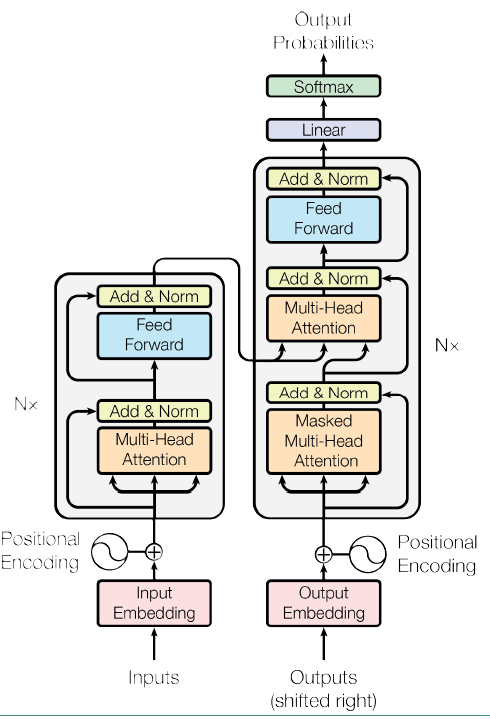由于Transformer模型最初是用在机器翻译任务上，所以它和seq2seq一样，也是一种encoder-decoder架构。
首先看左边的encoder部分，Nx表示有N层这样的Layer，每个Layer由两个sub-layer组成，分别是multi-head self-attention mechanism和fully-connected feed forward network。其中每个sub-layer都加了residual connection（其实残差网络不光可以相加，还可以相减，目的是可以有效的仅关注差异部分）和normalisation。输入部分是Word Embedding和position Embedding的按位sum。
Decoder和Encoder的结构类似，只是多了一层multi-head attention sub-layer，这里先明确一下decoder的输入输出和解码过程：
- 输出：对应i位置的输出词的概率分布。
- 输入：encoder的输出 & 对应i-1位置decoder的输出。所以第二层的attention不是self-attention，它的KV来自encoder，Q来自上一位置decoder的输出。
- masked multi-head Attention：第一个multi-head attention多加了一个mask，主要有两层作用：一是CNN的输入需要做Padding，由于Padding部分是无意义的，这个时候不能与position embedding做sum，所以需要将position embedding部分也mask为全零；二是因为训练时的output都是ground truth，所以需要将所预测的第i个位置之后的词统统mask掉，以确保预测第i个位置时不会接触到未来的信息。因为attention的Q要和每个K相乘，如果你在预测的时候允许模型接触到这个值，数据就泄露了。
Positional Encoding
Transformer抛弃了RNN，而RNN最大的优点就是在时间序列上对数据的抽象，而Transformer又是一种完全由CNN、MLP + Attention的架构，是一种位置不敏感的模型，虽然self-Attention能提取词与词之间的依赖关系，但是却不能提取词的绝对位置或者相对位置关系，所以作者提出将Positional Encoding之后与Word embedding做sum，以加入相对位置信息。这里主要介绍三种常用的Positional Encoding方法。
直接使用位置的one-hot编码
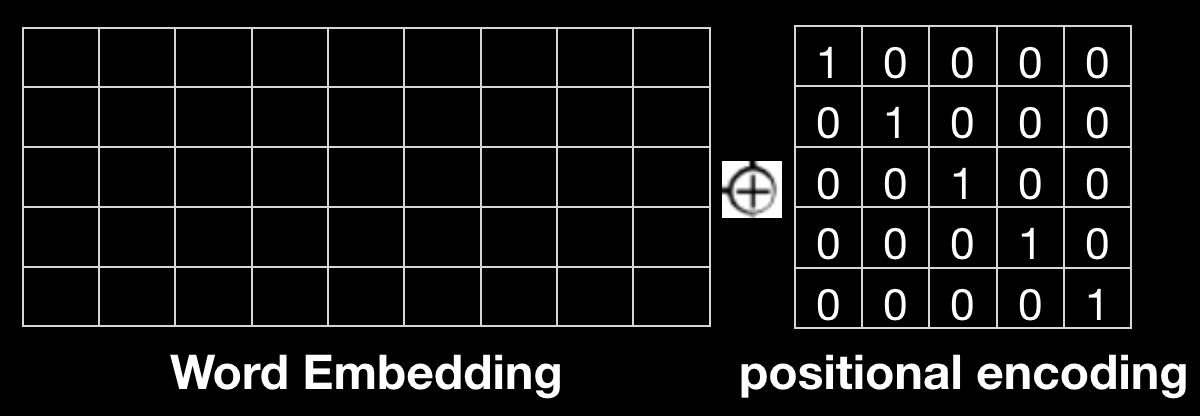这种方式形式简单易于理解，但是one-hot编码始终不具备语义化的数值表达，并且当sequence length过长时，one-hot编码过于稀疏，而且Word embedding与one-hot向量并不在同一数值空间内，所以一般情况下效果并不太好。
learned position embedding
word_embedding = tf.get_variable('word_embedding', [self.config.vocab_size, self.config.word_embedding_size])
word_embedding_inputs = tf.nn.embedding_lookup(word_embedding, self.input_x_word_idx)
position_embedding = tf.get_variable('position_embedding', [self.config.seq_length, self.config.position_embedding_size])
position_embedding_inputs = tf.nn.embedding_lookup(position_embedding, self.input_x_position_idx)
embedding_inputs = tf.sum([word_embedding_inputs, position_embedding_inputs], -1)
这是比较常用的方式，类似于Word embedding，使position也具备了语义化的数值表达。注意：keep dim 0 for padding token，and then position encoding zero vector。
sinusoidal position encoding
sinusoidal position encoding的计算公式如下所示，公式并不复杂：
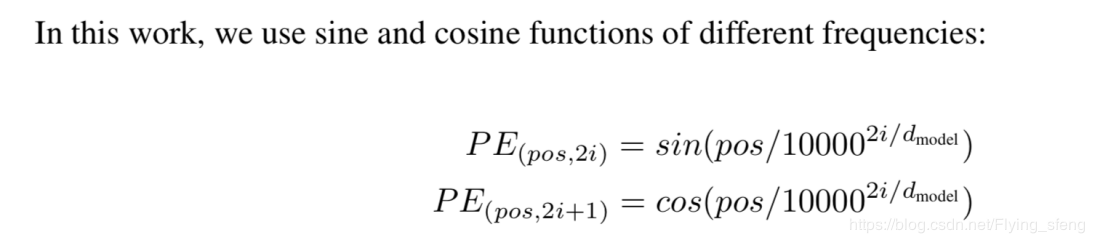pos表示位置，dmodel表示position encoding的向量维度，i表示向量的第i个位置元素（i取值范围为[0,dmodel/2]）。因此上述公式表示position encoding向量的偶数位置元素为sin值，奇数位置为cos值，并以此计算出整个position encoding向量。
这是一种相对位置编码，而Word embedding是绝对位置编码。大家试想一下，位置1和位置2的距离比位置3和位置10的距离更近，位置1和位置2与位置3和位置4都只相差1，这些关于位置的相对含义 如果仅通过绝对位置编码模型不一定能get到，因为使用Learned Positional Embedding编码，位置之间没有约束关系，我们只能期待它隐式地学到，而sinusoidal position encoding能够显示的让模型理解位置的相对关系。另外论文上说sinusoidal position encoding并不受限于序列长度，其可以在遇到训练集中未出现过的序列长度时仍能很好的“extrapolate”，即sinusoidal position encoding可以无限扩展到任意长度，但是这种解释有点牵强，因为在实际使用上过长的数据还是都被截断了的。
sin编码和cos编码之所以可以得到词语之间的相对位置，是因为PE(pos+k)可以被PEpos线性表示，感兴趣的同学可以证明一下，当pos分别取3和4的时候，PE4怎样由PE3线性表示。
（其实CNN也能提取到句子内部词与词之间的相对位置关系，但是受限于卷积核的大小，需要多层CNN解决）
Attention
multi-head attention是transformer的核心，模型图如下所示，也比较简单直观：
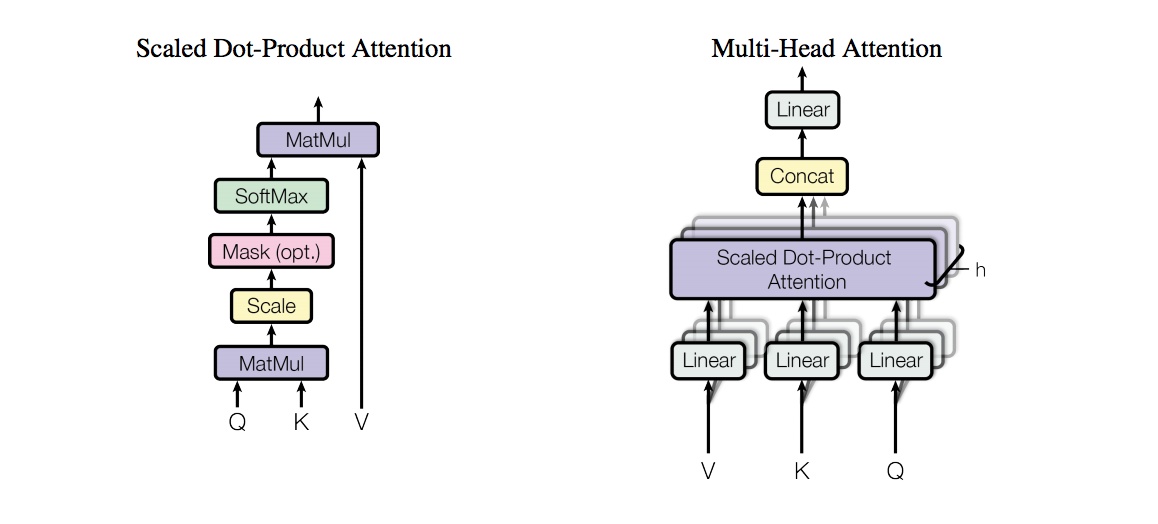
Scaled Dot-Product Attention
MLP难以学习向量内积以及特征组合变换（特征相乘），这也是为什么QQ-match模型最后必须用余弦相似度（向量内积）而不用MLP二分类来计算损失函数的原因，因为MLP二分类损失函数效果极差。
我们知道Attention的计算公式为：
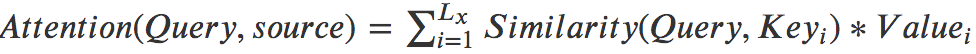其中Lx代表source中句子的sequence length。其实如果相似度计算使用向量点积的话，上式就变成了[softmax(Q · KT)] · V，然而点积的方法面临一个问题，假设K、Q的向量元素都是均值为0方差为1，那么当向量维度太大时，点积计算得到的内积结果会出现两极分化，这样在计算softmax时，结果都非常接近0和1，这样可能会导致梯度过小或消失，因此对向量内积除以根号下dk（dk是向量维度）来对内积结果进行缩放，这就是Scaled Dot-Product Attention：
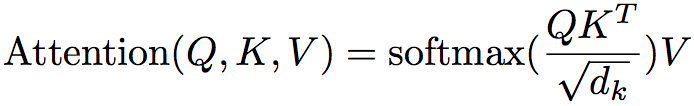对于self-attention，一方面能够很好地捕捉句子内部的长距离依赖，学习到句子的内部结构及语法，另一方面与单纯的词向量比，是一种更全局的表达。
Multi-Head Attention
即分别对Q、K、V进行h次不同的线性变换（h为head数），在每次线性变换中，对Q、K、V又都使用不同的权重矩阵（所以一共使用了3h个不同的权重矩阵），然后对每次线性变换的结果计算Attention，再将不同的attention结果拼接起来，最后再经过一次总的线性变换（h头线性变换的权重矩阵维度为dk/h，这样h头最后一维拼接后维度即还原为dk）。
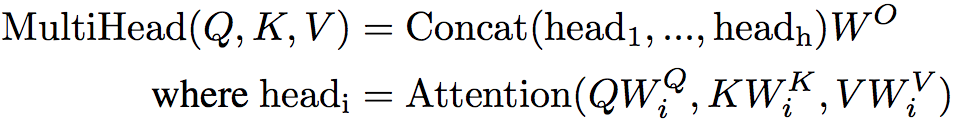
self.W=self.add_weight(name='W',
shape=(self.num_head,3,input_shape[2],self.output_dim),
initializer=self.kernel_initializer,
trainable=True)
self.Wo=self.add_weight(name='Wo',
shape=(self.num_head*self.output_dim,self.output_dim),
initializer=self.kernel_initializer,
trainable=True)
for i in range(1,self.W.shape[0]):
q=K.dot(x,self.W[i,0])
k=K.dot(x,self.W[i,1])
v=K.dot(x,self.W[i,2])
e=K.batch_dot(q,K.permute_dimensions(k,[0,2,1])) # 把k转置，并与q点乘
e=e/(self.output_dim**0.5)
e=K.softmax(e)
o=K.batch_dot(e,v)
outputs=K.concatenate([outputs,o]) # 最后一维上做拼接
z=K.dot(outputs,self.Wo)
为什么要使用Multi-Head Attention呢？ 其实Multi-Head Attention类似与卷积中的多个卷积核，在卷积神经网络中，我们认为不同的卷积核会捕获不同的局部信息，得到不同的feature map，在这里也是一样，我们认为Multi-Head Attention可以让模型从不同角度理解输入的序列。因为在进行映射时不共享权值，因此映射后的子空间是不同的，认为不同的子空间涵盖的信息是不一样的，这样最后拼接的向量涵盖的信息会更广。
Position-wise Feed-Forward
其实就是采用Relu激活函数的全连接神经网络，复习一下，128个神经元的单层全连接神经网络，其实就是拥有128个1x1卷积核的卷积神经网络。因为Multi-Head Attention的每个头都是独立运行，通过该层可以提炼出head之间的feature interaction。
LayerNorm
LN是和BN非常近似的一种归一化方法，不同的是BN取的是不同样本的同一个特征做归一化，而LN取的是同一个样本的不同特征。在BN和LN都能使用的场景中，BN的效果一般优于LN，原因是基于不同数据，同一特征得到的归一化特征更不容易损失信息。但是有些场景是不能使用BN的，当样本数很少时，比如说只有4个，这4个样本的均值和方差便不能反映全局的统计分布信息，所以基于少量样本的BN的效果会变得很差。在一些场景中，比如说硬件资源受限、RNN、在线学习等场景，BN是非常不适用的。这时候可以选择使用LN，LN得到的模型更稳定且能起到正则化的作用，并且LN将每个训练样本都归一化到了相同的分布上，所以从原理上讲，LN还能加速收敛。
具体就是，LN可以缓解Internal Covariate Shift问题，可以将数据分布拉到激活函数的非饱和区，具有权重/数据伸缩不变性的特点。起到缓解梯度消失/爆炸、加速训练、正则化的效果。
RNN可以展开成一个隐藏层共享参数的MLP，随着时间片的增多，展开后的MLP的层数也在增多，最终层数由输入数据的时间片的数量决定，所以RNN是一个动态的网络。在一个batch中，通常各个样本的长度都是不同的，当统计到比较靠后的时间片时，通常只有某几个样本还有数据，基于这几个样本的统计信息不能反映全局分布，所以这时BN的效果并不好。
下面来看MLP中的LN：H是一层中隐层节点的数量，l是MLP的层数，我们可以计算LN的归一化统计量：
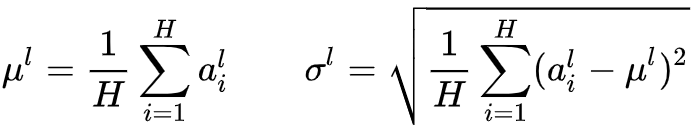通过均值方差，可以计算归一化后的值：
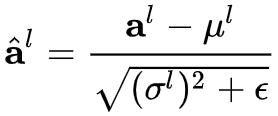其中e是一个很小的小数，防止除0。和BM一样，在LN中我们也需要一组可学习的参数来保证归一化操作不会破坏之前的信息，在LN中这组参数叫做增益（gain）和偏置（bias），注意g和b都是向量，最终LN的输出为：
