DeepFM
FM(Factorization Machine,因子分解机)主要是为了解决数据稀疏的情况下,特征两两组合的问题。后人基于FM模型结合深度学习,进行了很多尝试,比如:
- FNN(Factorization-machine supported Neural Network),该模型先预训练FM,然后把得到的隐向量作为embedding的初始值,应用到DNN网络,因此该模型严重受限于FM的能力,并且FM的误差会级联传递下去。
- PNN(Product-based Neural Network),在embedding层和MLP之间加入Product层,Product层就是将embedding后的特征向量两两内积(向量内积又叫inner product,其结果就是两向量相乘,是一个值;向量外积又叫outer product,一个n维向量和一个m维向量的外积结果是一个n x m矩阵,也有些地方认为向量外积就是按位点乘)。也只能捕获两两特征之间的交互关系。
- 对于FM来说,先对特征的每一个field查找一个embedding向量,再进行交叉(点乘)。而对于FFM(Field-aware Factorization Machine)来说,先把特征之间的所有field取值两两组合(cross)好,再对于每一种组合去查找embedding向量表。
Wide & Deep model,之前讲过,wide部分仍然需要专家级的特征工程,才能知道应该把哪些特征之间进行cross product。DeepFM(Factorization-Machine based neural network)模型能够端到端的学习all-order的特征交互,而不需要任何特征工程(一个特征叫1-order,两个特征cross叫2-order,n个特征cross叫n-order)。它通过将FM与DNN集成,FM负责model low-order特征交互,DNN负责model high-order特征交互。
模型架构
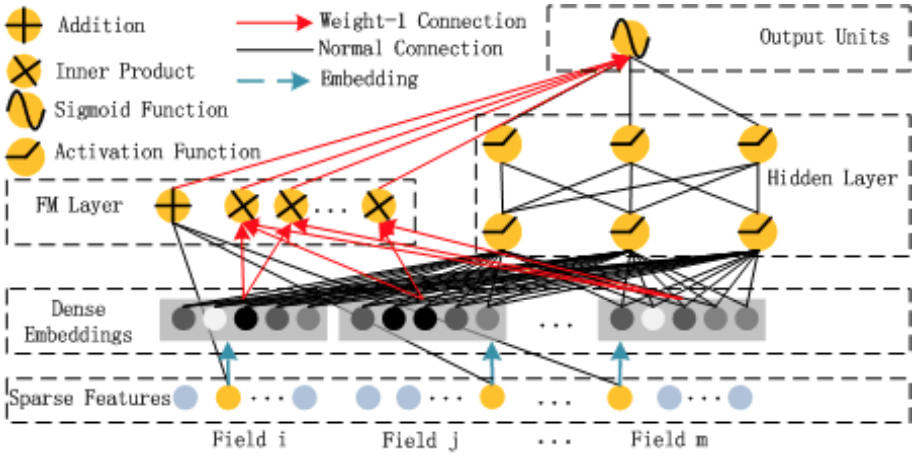 Addition其实代表concat。
Addition其实代表concat。
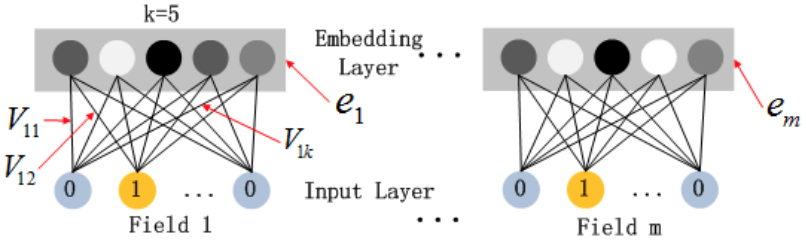 FM部分与DNN部分共享同样的特征embedding,FM中的特征隐向量V同时作为了embedding向量。这样使得训练完成后的特征embedding能够同时准确的handle low and high-order特征交互。假设我们的embedding向量维度k=5,首先,对于输入的一条记录,同一个field只有一个位置是1,那么在由输入得到dense vector的过程中,输入层只有一个神经元起作用,得到的dense vector其实就是输入层到embedding层该神经元相连的五条线的权重,即vi1、vi2、vi3、vi4、vi5,这五个值组合起来就是我们在FM中所提到的Vi。在FM部分和DNN部分,这一块是共享权重的,对同一个特征来说,得到的Vi是相同的。
FM部分与DNN部分共享同样的特征embedding,FM中的特征隐向量V同时作为了embedding向量。这样使得训练完成后的特征embedding能够同时准确的handle low and high-order特征交互。假设我们的embedding向量维度k=5,首先,对于输入的一条记录,同一个field只有一个位置是1,那么在由输入得到dense vector的过程中,输入层只有一个神经元起作用,得到的dense vector其实就是输入层到embedding层该神经元相连的五条线的权重,即vi1、vi2、vi3、vi4、vi5,这五个值组合起来就是我们在FM中所提到的Vi。在FM部分和DNN部分,这一块是共享权重的,对同一个特征来说,得到的Vi是相同的。
在FM中,特征i和j的交互是通过他们的隐向量计算内积完成。只要特征i或j出现在了训练数据中,FM就能够训练特征i或j的隐向量,然后特征i和j的交互直接通过隐向量内积得到。而对于之前的模型,想要学习特征i和j的交互,就必须特征i和j同时出现在同一个训练样本中,当数据稀疏时,这是不可能的。因此,对于训练数据中从未出现过的特征交互,FM也能很好的学习。
对于FM部分,模型表达式如下所示:
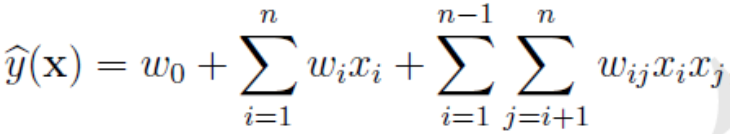 由此看出,模型的计算复杂度为O(n*n),n为特征数量,为了简化计算,我们引入辅助向量V(维度为k),并将参数Wij改写为:
由此看出,模型的计算复杂度为O(n*n),n为特征数量,为了简化计算,我们引入辅助向量V(维度为k),并将参数Wij改写为:
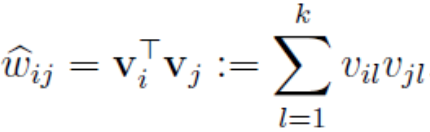 然后我们可以得到如下证明:
然后我们可以得到如下证明:
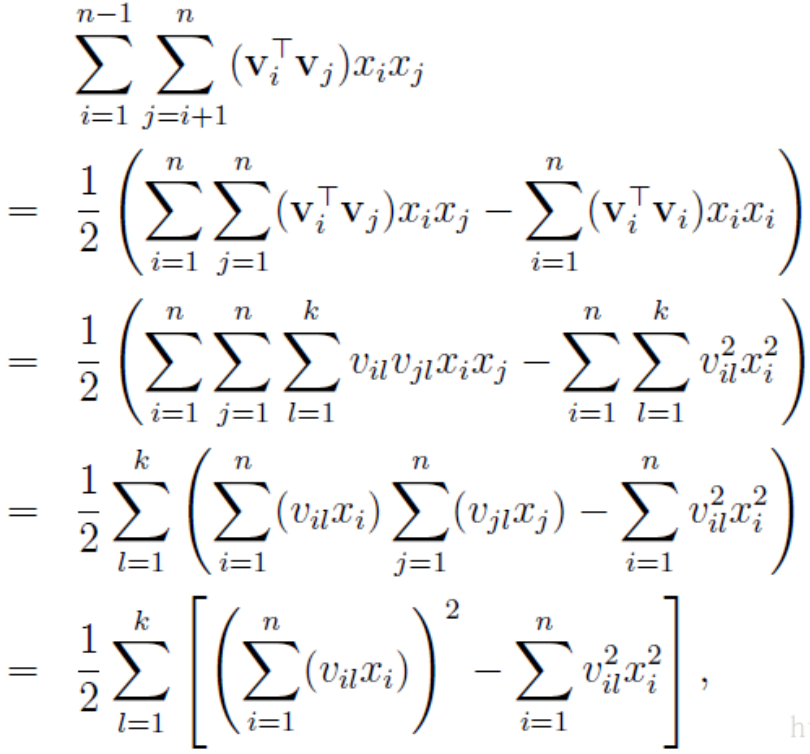 关于第一步的变换过程,证明如下:
关于第一步的变换过程,证明如下:
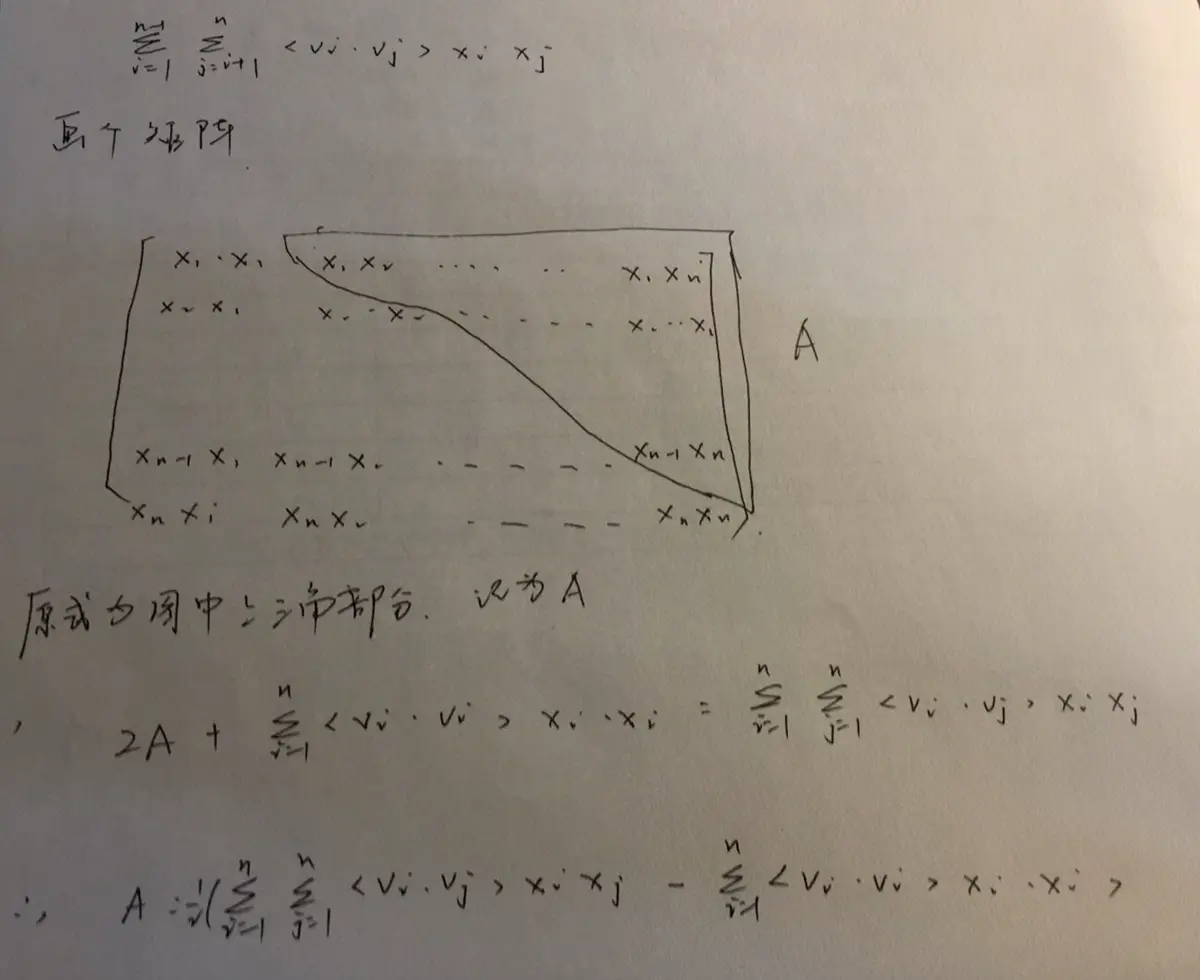 可以看出,变换后的计算复杂度为O(n),大大简化了计算。
可以看出,变换后的计算复杂度为O(n),大大简化了计算。
下面我们将结合代码进行讲解。
输入层
#feat_index是特征的一个序号,主要用于通过embedding_lookup选择我们的embedding。
feat_index = tf.placeholder(tf.int32, shape=[None,field_size], name='feat_index')
#feat_value是对应的特征值,如果是离散特征的话,就是1,如果不是离散特征的话,就保留原来的特征值。
feat_value = tf.placeholder(tf.float32, shape=[None,field_size], name='feat_value')
label = tf.placeholder(tf.float32,shape=[None,1], name='label')
embedding层
#weights['feature_embeddings']矩阵中的每一行其实就是FM中的Vik,他的shape是f x k。f为所有特征one-hot后的总大小,K代表dense vector的维度。
weights['feature_embeddings'] = tf.Variable(tf.random_normal([feature_size,embedding_size],0.0,0.01))
#weights['feature_bias']是FM中的一次项的权重。
weights['feature_bias'] = tf.Variable(tf.random_normal([feature_size,1],0.0,1.0))
embeddings = tf.nn.embedding_lookup(weights['feature_embeddings'],feat_index) # N x field_size x k
feat_value = tf.reshape(feat_value,shape=[-1,field_size,1])
#这里相当于对实值特征进行了一次repeat操作,由1个数repeat为一个k维向量。该实值K维向量乘以embeddings,相当于先进行了一次线性变换,这样做是有好处的,将实数值映射到与embeddings同一向量空间中,利于模型训练。
embeddings = tf.multiply(embeddings,feat_value)
DNN part
y_deep = tf.reshape(embeddings, shape=[-1,self.field_size * self.embedding_size]) #Flatten
y_deep = tf.layers.dense(y_deep, activation="relu", use_bias=True)
FM part
# 1-order
y_first_order = tf.nn.embedding_lookup(weights['feature_bias'],feat_index)
y_first_order = tf.reduce_sum(tf.multiply(y_first_order,feat_value),2) # None * f,进行了sum pooling操作,每一维特征变成了一个值
# 2-order
summed_features_emb = tf.reduce_sum(embeddings,1) # None * k
summed_features_emb_square = tf.square(summed_features_emb) # None * k
squared_features_emb = tf.square(embeddings)
squared_sum_features_emb = tf.reduce_sum(squared_features_emb,1) # None * k
fm_second_order = 0.5 * tf.subtract(summed_features_emb_square,squared_sum_features_emb)
训练
concat_input = tf.concat([y_first_order, y_second_order, y_deep], axis=1)
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=self.logits, labels=label))
optimizer = tf.train.AdamOptimizer(learning_rate=1e-3).minimize(loss)
DCN
在DeepFM中,FM部分只用到了2-order的特征交互,deep部分由于是隐式的构造cross features,所以对于某些类型的特征交互,并不能有效的学习。DCN(Deep & Cross Network),仍然和DeepFM一样沿用wide & deep架构,deep部分仍然是MLP捕获高纬度非线性特征交互,而wide部分改成了Cross Network,其每一层显示应用了特征交叉,事实上,正是由于Cross Network的特殊网络结构,使得the degree of cross features to grow with layer depth。DCN模型架构如下所示:
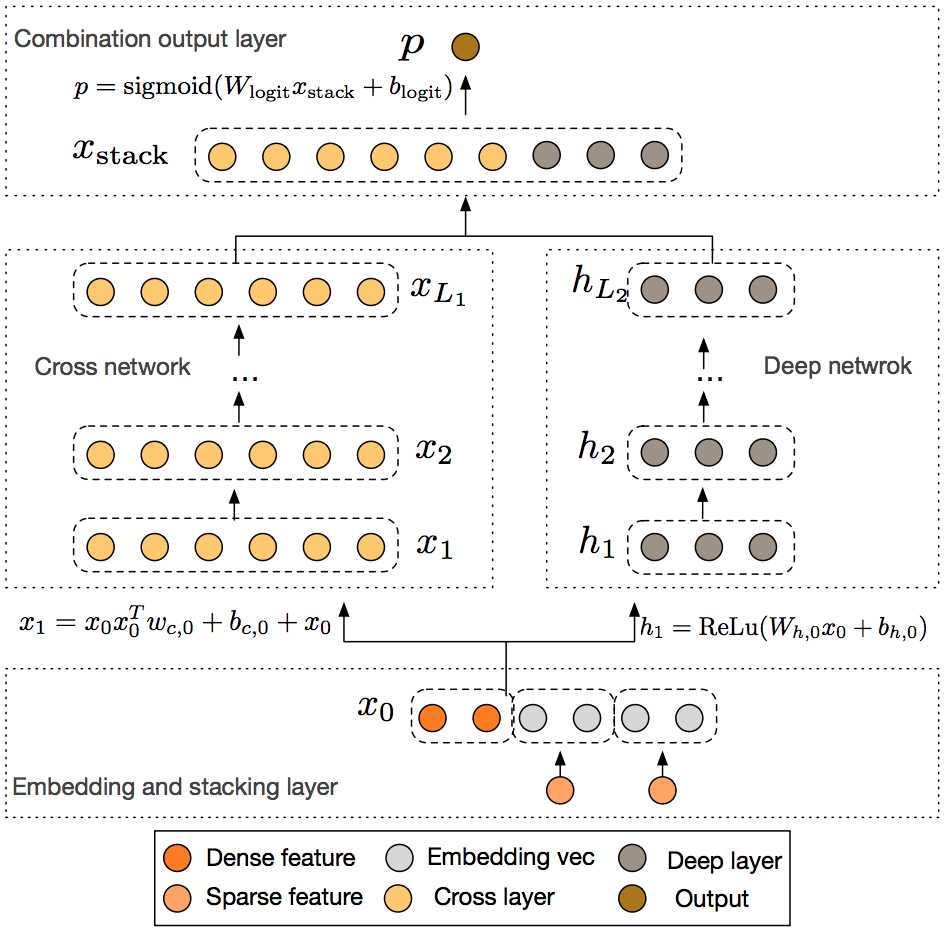
Cross Network
Cross Network的关键思想就是,通过一种高效的递归方式显示的model线性特征交叉,公式如下所示:
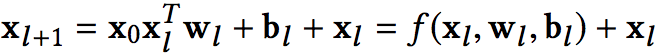 这样层层递归下去,并且上下层特征通过残差网络相连接。论文中的定理与证明过程都比较晦涩,为了直观清晰地讲解清楚,我们直接看一个具体的例子:假设Cross Network有2层,
这样层层递归下去,并且上下层特征通过残差网络相连接。论文中的定理与证明过程都比较晦涩,为了直观清晰地讲解清楚,我们直接看一个具体的例子:假设Cross Network有2层,
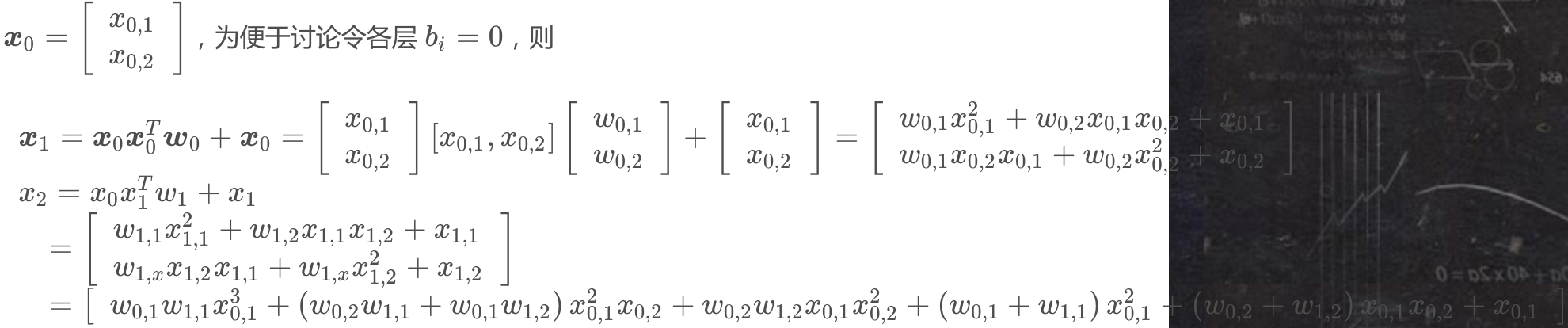 可以看到X1包含了原始特征x01,x02从一阶到二阶的所有可能的交叉组合,而X2包含了原始特征x01,x02从一阶到三阶的所有可能的交叉组合,但是每层也只引入了两个参数。随着网络层数的不断加深,也就包含了更加高阶的所有可能的交叉组合,但是网络参数也只是线性增长,而不是指数增长。综上,Cross Network的特性如下:
可以看到X1包含了原始特征x01,x02从一阶到二阶的所有可能的交叉组合,而X2包含了原始特征x01,x02从一阶到三阶的所有可能的交叉组合,但是每层也只引入了两个参数。随着网络层数的不断加深,也就包含了更加高阶的所有可能的交叉组合,但是网络参数也只是线性增长,而不是指数增长。综上,Cross Network的特性如下:
- 有限高阶。叉乘阶数由网络深度决定,深度Lc对应最高Lc+1阶的叉乘。
- 自动叉乘。Cross Network的输出包含了原始特征从一阶(即本身)到Lc+1阶的所有叉乘组合,而模型参数量仅仅随网络深度成线性增长:2 x d x Lc,d为特征数量。 3. 参数共享。不同叉乘项对应的权重不同,但并非每个叉乘组合对应独立的权重(否则,指数数量将是指数级),通过参数共享,有效降低了Cross Network的参数量。
- 泛化性。参数共享还使得模型有更强的泛化性和鲁棒性。例如,如果独立训练权重(不共享参数),当训练集中xi≠0⋂xj≠0x这个叉乘特征没有出现,那么对应权重肯定是零,而参数共享则不会使得其为0,这样使得预测时能够有效应对训练集中没有出现的叉乘组合。
DCN核心代码如下:
#输入层
self.feat_index = tf.placeholder(tf.int32,shape=[None,None],name='feat_index')
self.feat_value = tf.placeholder(tf.float32,shape=[None,None],name='feat_value')
self.numeric_value = tf.placeholder(tf.float32,[None,None],name='num_value')
self.label = tf.placeholder(tf.float32,shape=[None,1],name='label')
#embedding & concat
self.embeddings = tf.nn.embedding_lookup(self.weights['feature_embeddings'],self.feat_index) # N * F * K
feat_value = tf.reshape(self.feat_value,shape=[-1,self.field_size,1])
self.embeddings = tf.multiply(self.embeddings,feat_value)
self.x0 = tf.concat([self.numeric_value,tf.reshape(self.embeddings,shape=[-1,self.field_size * self.embedding_size])],axis=1)
#deep part
self.y_deep = tf.layers.dense(self.x0, activation="relu", use_bias=True)
#cross part
self._x0 = tf.reshape(self.x0, (-1, self.total_size, 1))
x_l = self._x0
for l in range(self.cross_layer_num):
x_l = tf.tensordot(tf.matmul(self._x0, x_l, transpose_b=True),self.weights["cross_layer_%d" % l],1) + self.weights["cross_bias_%d" % l] + x_l
self.total_size = self.field_size * self.embedding_size + self.numeric_feature_size
self.cross_network_out = tf.reshape(x_l, (-1, self.total_size)) # 进行了sum pooling操作,每一维特征变成了一个值
#训练
concat_input = tf.concat([self.cross_network_out, self.y_deep], axis=1)
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=self.logits, labels=label))
optimizer = tf.train.AdamOptimizer(learning_rate=1e-3).minimize(loss)
XDeepFM
DCN的Cross层接在Embedding层之后,虽然可以显示自动构造有限高阶特征交叉,但它是以bit-wise的方式。即假设Age Field对应嵌入向量<a1,b1,c1>,Occupation Field对应嵌入向量<a2,b2,c2>,在Cross层,a1,b1,c1,a2,b2,c2会拼接后直接作为输入,这样就意识不到Field vector的概念。Cross 以嵌入向量中的单个bit为最细粒度,而FM的精髓是以向量为最细粒度学习相关性,即vector-wise。xDeepFM的动机,正是将FM的vector-wise的思想引入Cross部分。XDeepFM采用了CIN(Compressed Interaction Network,压缩交互网络)来做到这件事情。其网络结构如下:
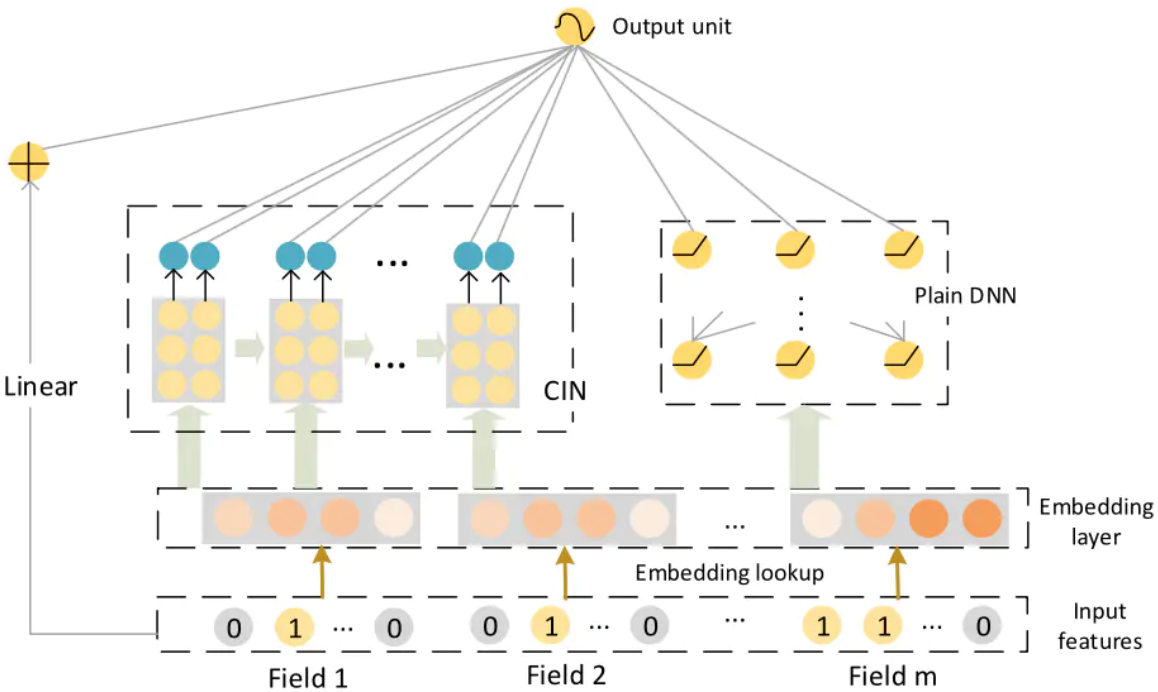 Linear部分以及Plain DNN部分与DeepFM一样,核心的就是CIN。CIN网络的宏观架构如下:
Linear部分以及Plain DNN部分与DeepFM一样,核心的就是CIN。CIN网络的宏观架构如下:
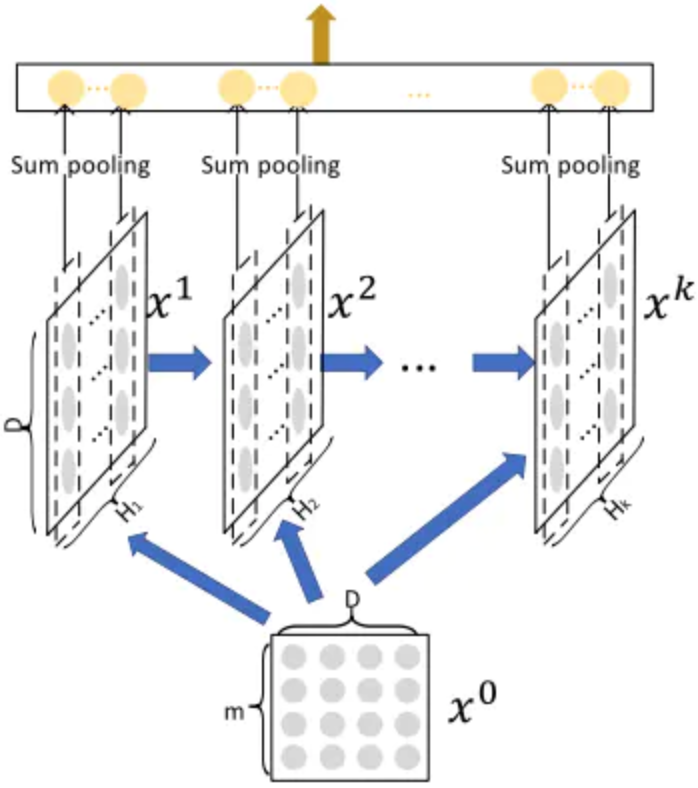 这里的X0为原始特征embedding后的向量矩阵,m是filed size,D是embedding size。不难看出,CIN的结构与RNN很是类似,即每一层的状态是由前一层隐层状态X的值与一个额外的输入数据计算所得,不同的是:CIN中不同层的参数是不一样的,而在RNN中是相同的;RNN中每次额外的输入数据是不一样的,而CIN中额外的输入数据是固定的,始终是X0。具体计算过程如下图:
这里的X0为原始特征embedding后的向量矩阵,m是filed size,D是embedding size。不难看出,CIN的结构与RNN很是类似,即每一层的状态是由前一层隐层状态X的值与一个额外的输入数据计算所得,不同的是:CIN中不同层的参数是不一样的,而在RNN中是相同的;RNN中每次额外的输入数据是不一样的,而CIN中额外的输入数据是固定的,始终是X0。具体计算过程如下图:
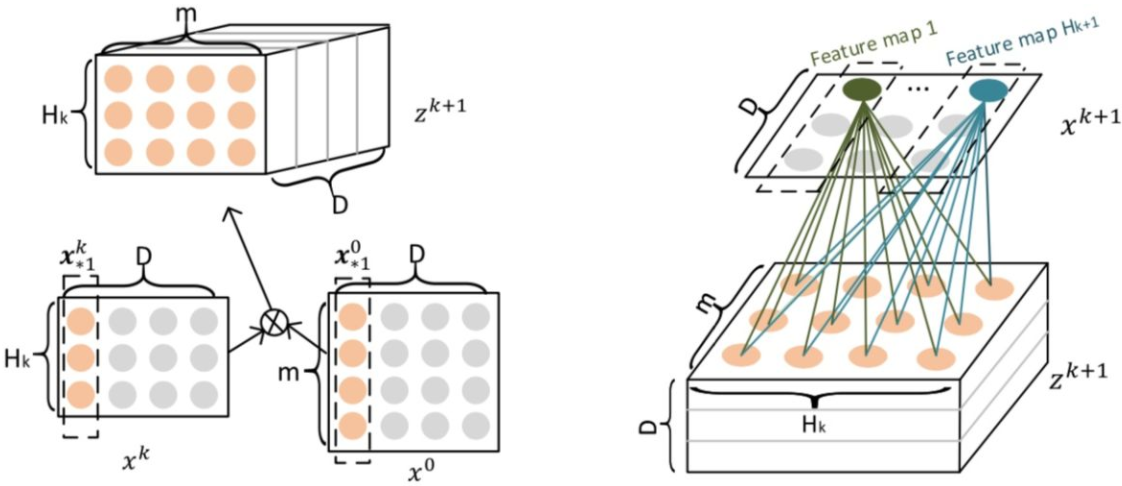
 相当于用Hk+1个尺寸为m x Hk的卷积核进行卷积操作。
相当于用Hk+1个尺寸为m x Hk的卷积核进行卷积操作。
CIN与DCN中Cross层的设计动机是相似的,Cross层的input也是前一层加X0,其实目的都是自动构造有限高阶特征交叉。如第一层:
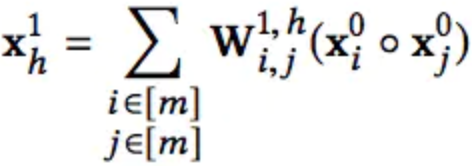 第二层:
第二层:
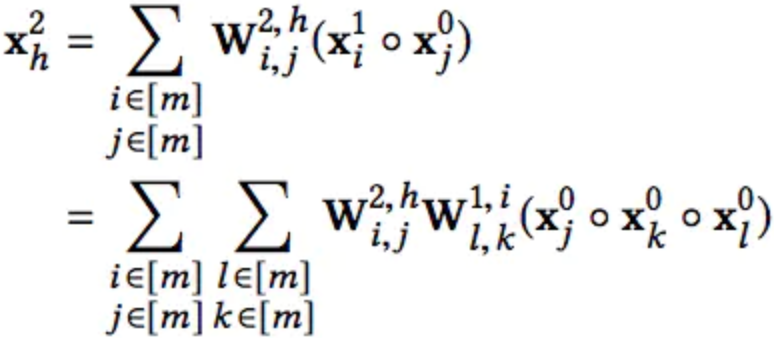 第K-1层:
第K-1层:
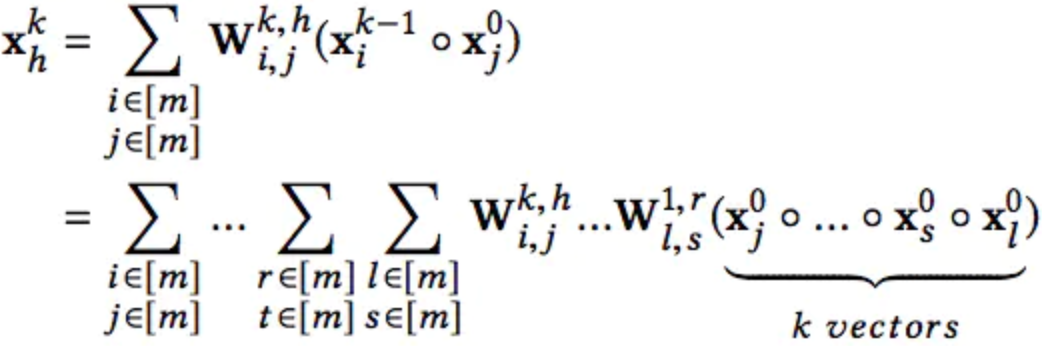 不过CIN与Cross还是有几点差异的:
不过CIN与Cross还是有几点差异的:
- Cross是bit-wise的,而CIN是vector-wise的。
- 在第l层,Cross包含从1阶~l+1阶的所有组合特征,而CIN只包含l+1阶的组合特征。所以CIN需要把每一层输出都concat起来。
- Cross在输出层输出全部结果,而CIN在每层都输出中间结果。中间结果经过sum pooling后到输出层。